C++超详细分析优化排序算法之堆排序

堆排序，学习了整整一天才把这个排序彻底搞明白……

首先第一点，堆排序是直接选择排序的一种优化排序算法。由于直接排序算法的遍历次数过多，导致直接排序算法的时间复杂度为O(N^2)，不适合排大量数据，堆排序应运而生。

堆排序（Heap Sort）进行的改进是能够保存一部分在每次遍历整个数组找出最大（小）值、次大（小）值，主要利用的就是完全二叉树这种数据结构。（后面说是如何保存这些数据的）

堆排序最重要的知识点无非两个：

1、向下调整算法

2、堆的逻辑结构是一棵完全二叉树

先从定义开始学习：

向下调整算法：顾名思义就是从上到下进行数据的调整，可以将完全二叉树调整为最大堆与最小堆（这两种堆也同时被称为“大顶堆”和“小顶堆”）这种算法的前提是：根节点的左右两棵子树均以建成最大（小）堆。

最大堆：所有的父节点都大于子结点

最小堆：所有的父节点都小于子结点

完全二叉树：从上到下、从左到右依次排列的一种树（即从第一层到第n-1层都是满的，只有第n层不满且从左到右排列数据）

（以建小堆为例）看一种典型的示例：

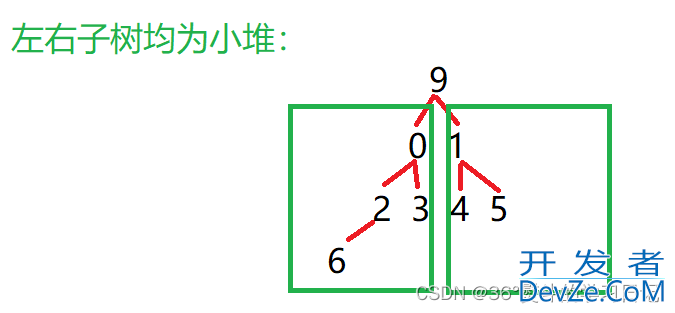
向下调整算法就是处理这种完全二叉树的一种算法，经过这种算法可将此数组建成最小堆。

先从根节点开始处理：

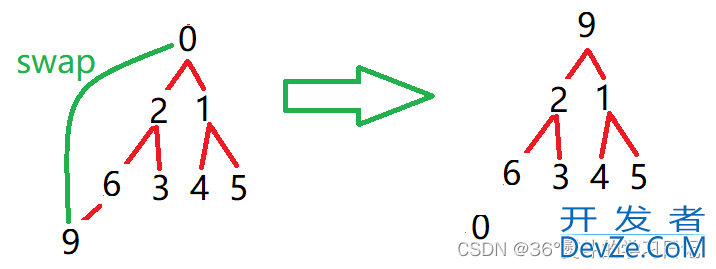
9 为父（根）节点，0，1都是其子节点，0 < 1；所以将0与9作一次交换；父节点同时下移至子节点，子节点变为新父节点的子节点：（p = parent, c = child）

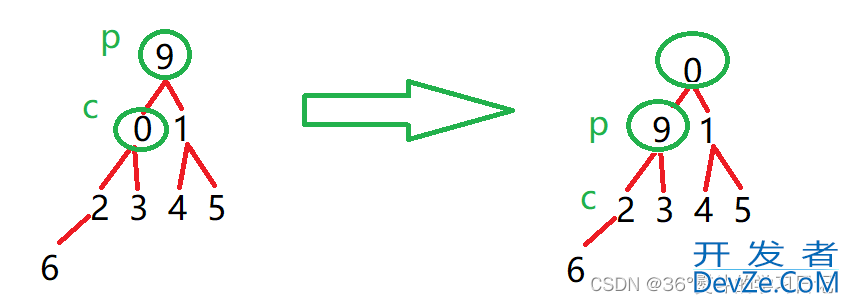
9 为父（根）节点，2，3都是其子节点，2 < 3；所以将2与9作一次交换；父节点同时下移至子节点，子节点变为新父节点的子节点：

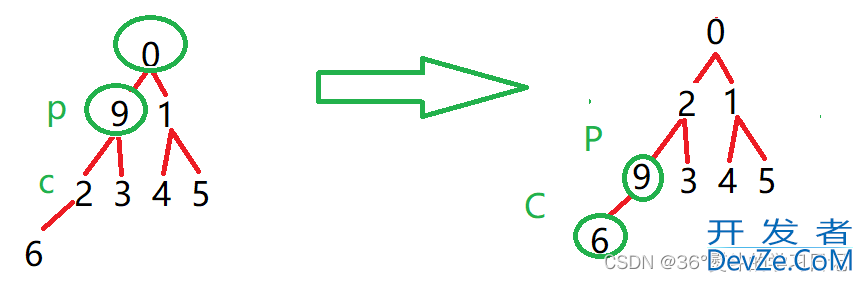
9 为父（根）节点，6 是其子节点，6< 9；所以将6与9作一次交换；父节点同时下移至子节点，子节点变为新父节点的子节点：

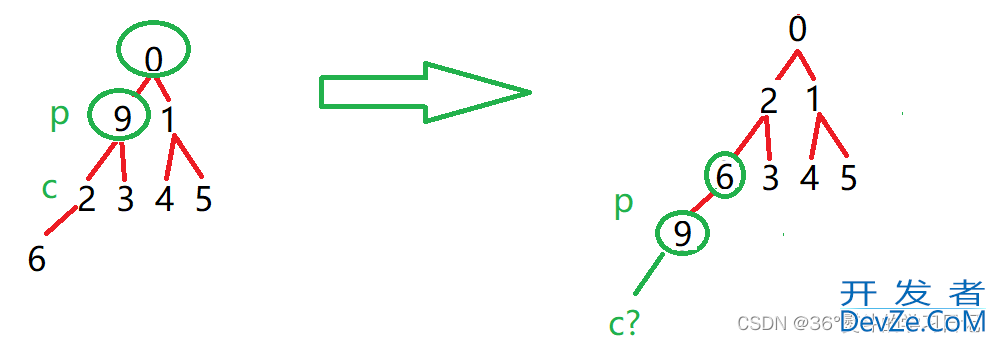
发现此时新的子节点已经越界，故停止向下调整；整个堆现已完成建堆成为最小堆！

这便是所谓的“向下调整算法”。

了解了以上知识后，还得知道父节点与子结点的表示方法：

leftchild = parent * 2 + 1;

rightchiljsd = parent * 2 + 2;

parent = (leftchild - 1) /2;

下面代码实战：

//向下调整：
//根节点左右子树必须已经成堆
void AdjustDown(int a[], int n, int parent)
{
	int child = parent * 2 + 1;
	//左孩子不能越界
	while (child < n)
	{
		//如果只有左孩子，那就不用判断两个孩子的大小，直接判断左孩子和父亲的大小
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		//向下调整
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = paren开发者_JS培训t * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

简单的交换函数：

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

堆排序的思想现在已经有了雏形：

将一个数组想象成堆，建堆，然后将堆顶最大（小）值置于堆底作为有序数据，这时会新形成一个堆，比之前的堆少一个数据，并且只有根节点的那棵小树未成堆，左右子树已形成大（小）堆，用一次向下调整算法即可将新堆再次建成最大（小）堆。

现在的问题是我们选择建一个最大堆还是最小堆呢？

我们不妨假设建了最小堆，也即上面我们刚刚构建好的堆：

不难发现这样是将最小值筛选出来，再向下调整，选出次小值，这样一来会得到降序的一个数组，反之，若使用最大堆，会得到一个升序的数组。

我们建大堆来得到一个升序数组，现有此无序数组：

//数组
int a[] = { 5,9,6,1,7,2,0,4,3,8 };
//元素个数
int n = (int)sizeof(a) / sizeof(a[0]);

第一步就是建堆：

我们会发现：这样“不听话”的数组显然不符合向下调整算法的前提条件，所以我们可以从这个数组中找能用这个算法的地方：从后向前去调整，最后一个叶子节点？一个数据，不需要调整；

最后一个父节点？他将会有0-2个子节点，而且只有这三个数据，不管怎么“不听话&rdquojavascript;，这个最小单位会满足“根的左右子树成堆”的这个条件，下一次再将这个父节点-1，即可实现对前一个父节点进行向下调整，循环此步骤直至真正的根节点，这时整个数组会被建成最大堆。

void HeapSort(int a[], int n)
{
    //建堆
	int parent = (n - 1 - 1) / 2;
	while (parent >= 0)
	{
		AdjustDown(a, n, parent);
		parent--;
	}
}

第二步就是排序：

建成堆后，我们需要进行数据的交换形成有序数据区。

void HeapSort(int a[], int n)
{
    //建堆
	int parent = (n - 1 - 1) / 2;
	while (parent >= 0)
	{
		AdjustDown(a, n, parent);
		parent--;
	}
	//已经成最大堆,不用再从最后一个父节点建堆
	//每次只用改变根节点的堆（根左右堆已为最大堆）
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

堆排序完毕！

整个代码分享：

#include <stdio.h>
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
//向下调整：
//根节点左右子树必须已经成堆
void rlPDLWDIAdjustDown(int a[], int n, int parent)
{
	int child = parent * 2 + 1;
	//左孩子不能越界
	while (child < n)
	{
		//如果只有左孩子，那就不用判断两个孩子的大小，直接判断左孩子和父亲的大小
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		//向下调整
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
vpythonoid HeapSort(int a[], int n)
{
	int parent = (n - 1 - 1) / 2;
	while (parent >= 0)
	{
		AdjustDown(a, n, parent);
		parent--;
	}
	//已经成最大堆,不用再从最后一个父节点建堆
	//每次只用改变根节点的堆（根左右堆已为最大堆）
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
void print(int* a, int n)
{
	int i = 0;
	for (i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}
int main()
{
	int a[] = { 5,9,6,1,7,2,0,4,3,8 };
	int n = (int)sizeof(a) / sizeof(a[0]);
	HeapSort(a, n);
	print(a, n);
	return 0;
}

到此这篇关于C++超详细分析优化排序算法之堆排序的文章就介绍到这了,更多相关C++编程客栈堆排序内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！