目录
- mao和set模拟实现
- 模拟实现
- 取K的仿函数
- Insert
- 迭代器
- begin和end
- ++和--
- operator[]
- 完整代码
- set.h
- map.h
- rbtree.h
- 总结
mao和set模拟实现
STL map和set只是包含了几个头文件

主要在选中的这个文件里,打开之后我们可以看到红黑树
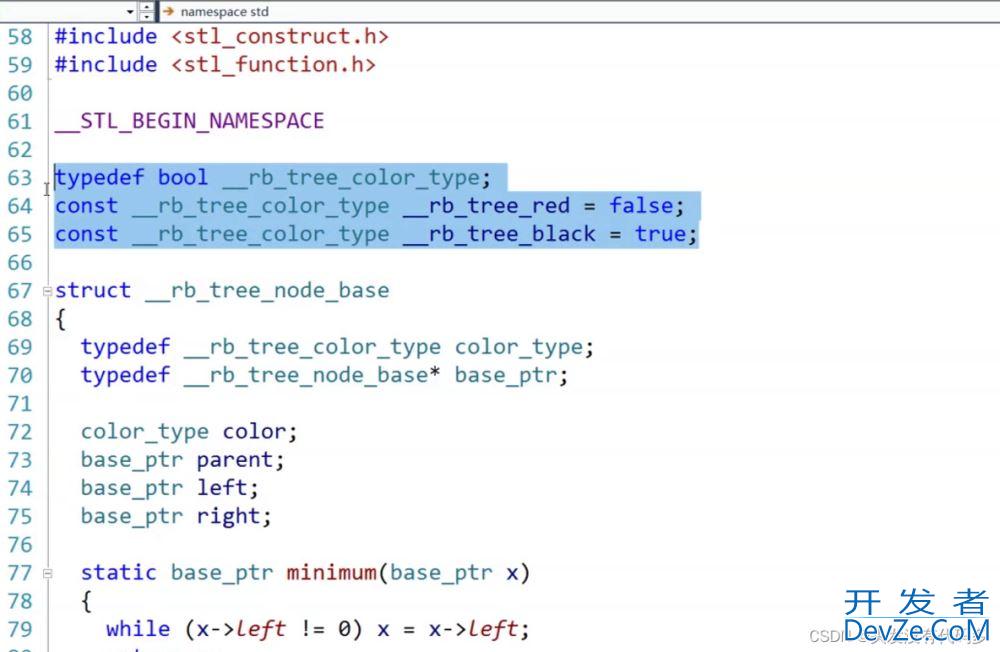
用红黑树实现map和set
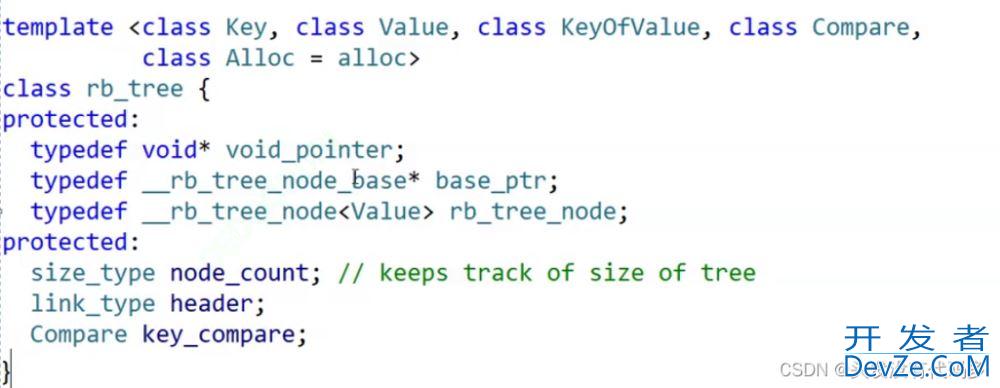
set的主要实现
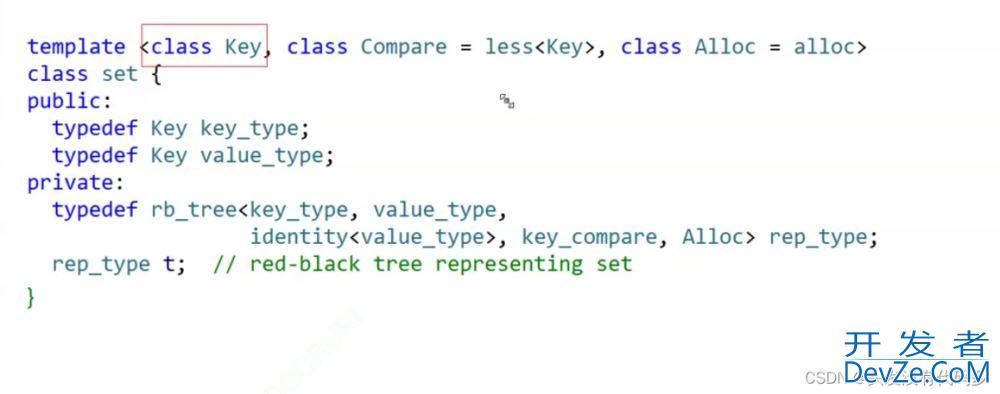
set里面的value type和key type都是KEY
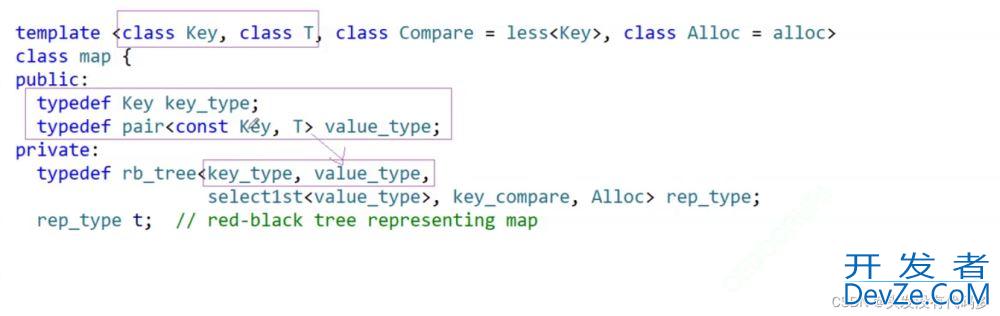
map里面的value type是pair,key type是KEY
这里用一颗泛型结构的RBTree,通过不同的实例化参数,实现出了map和set。
模拟实现
这里不用说明红黑树是K还是KV,用T来决定红黑树,使用时T是什么,红黑树就是什么

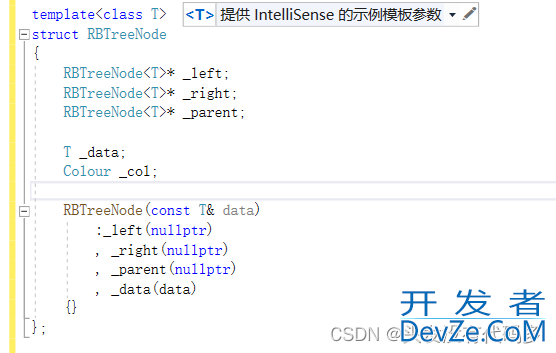
如Map传的是pair,T就是pair,Set传的是K,T就是K
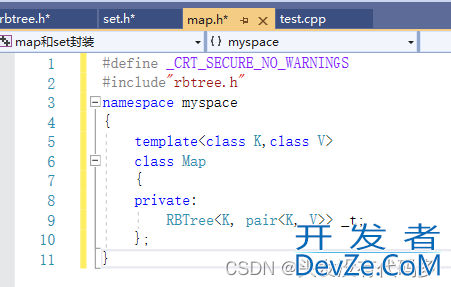
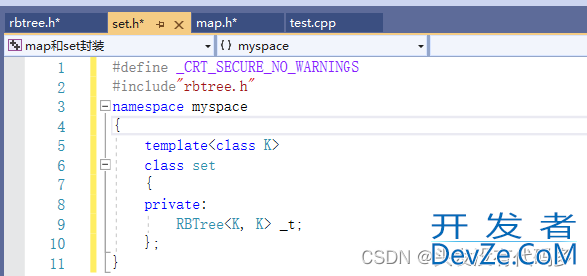
T传给了节点里面的data,上面传参传K的原因是find函数要用到,find是通过K去进行查找。
Insert插入数据的时候要比较数据的大小选择合适的位置插入,但这里data是T类型,对于set可直接比编程客栈较,而map传过来的是pair,如果比较pair就要比较first和second,这种不满足我们的需求,因为比较的时候既要满足set也要满足Map.
我们用仿函数来满足这种要求,这里仿函数是把T里面的k取出来,pair的K就是first

取K的仿函数
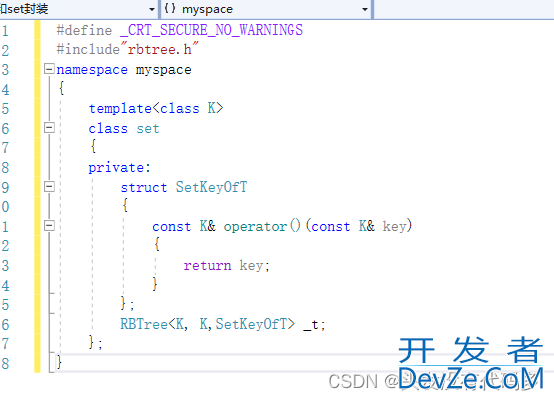
对于set而言,直接返回就行
对于map而言,就要取first
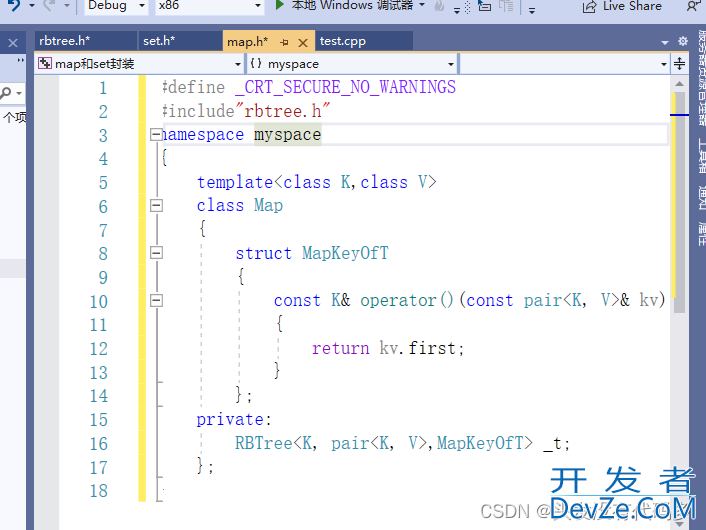
之后修改rbtree.h,创建一个仿函数对象,这个对象是什么类型的就根据什么类型取比较即可
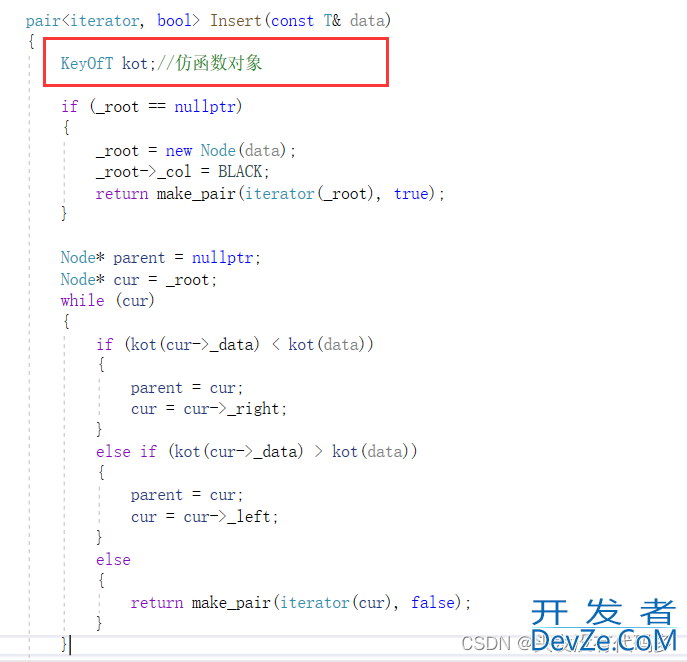
Insert
对于Map而言,_t是RBTree类型,Map的insert只需调用红黑树的Insert即可
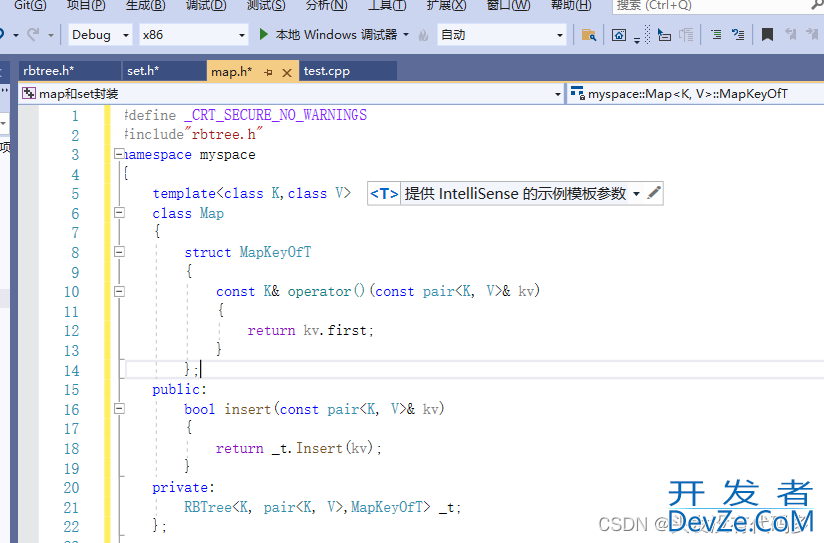
set也一样
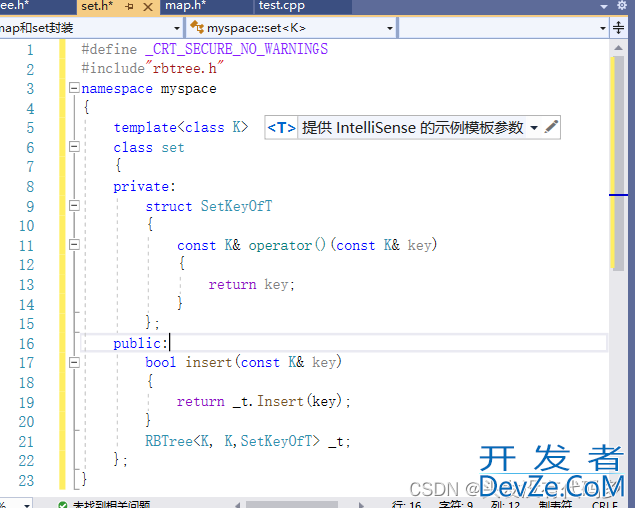
迭代器
迭代器也依靠红黑树的迭代器实现,tyoename作用,告诉编译器是要把类型进行重命名
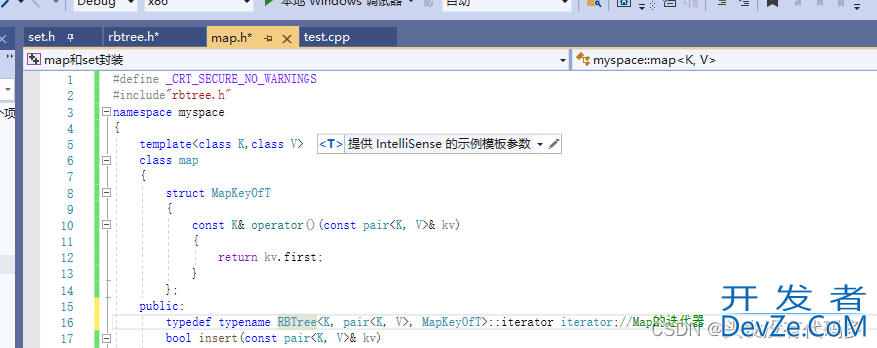
以下是红黑树的迭代器
enum Colour
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Colour _col;
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
{}
};
template<class T, class Ref, class Ptr>
struct __RBTreeIterator//迭代器
{
typedef RBTreeNode<T> Node;
typedef __RBTreeIterator<T, Ref, Ptr> Self;
Node* _node;
__RBTreeIterator(Node* node)//构造
:_node(node)
{}
Ref operator*()//返回引用
{
return _node->_data;
}
Ptr operator->()//返回指针
{
return &_node->_data;
}
bool operator!=(const Self& s) const
{
return _node != s._node;
}
bool operator==(const Self& s) const
{
return _node == s._node;
}
};
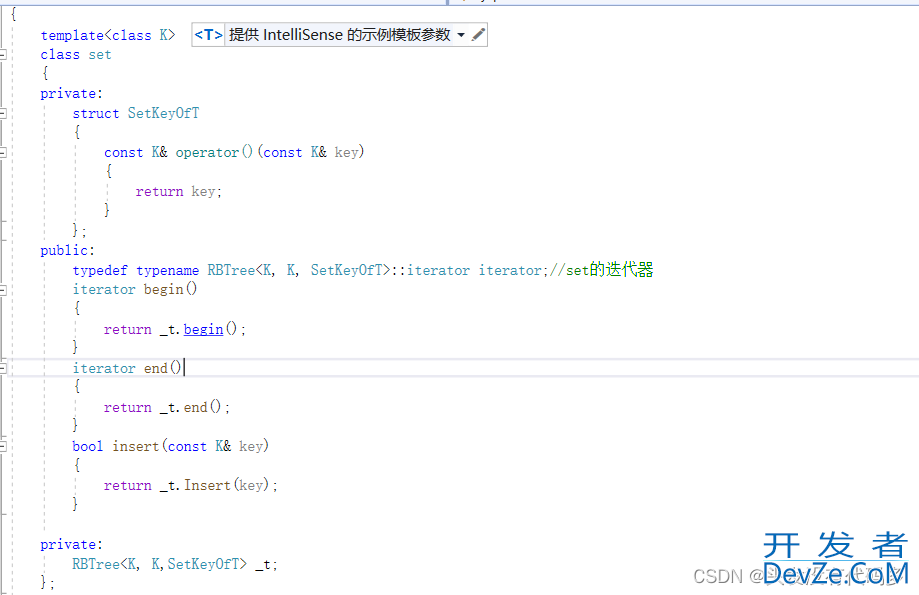
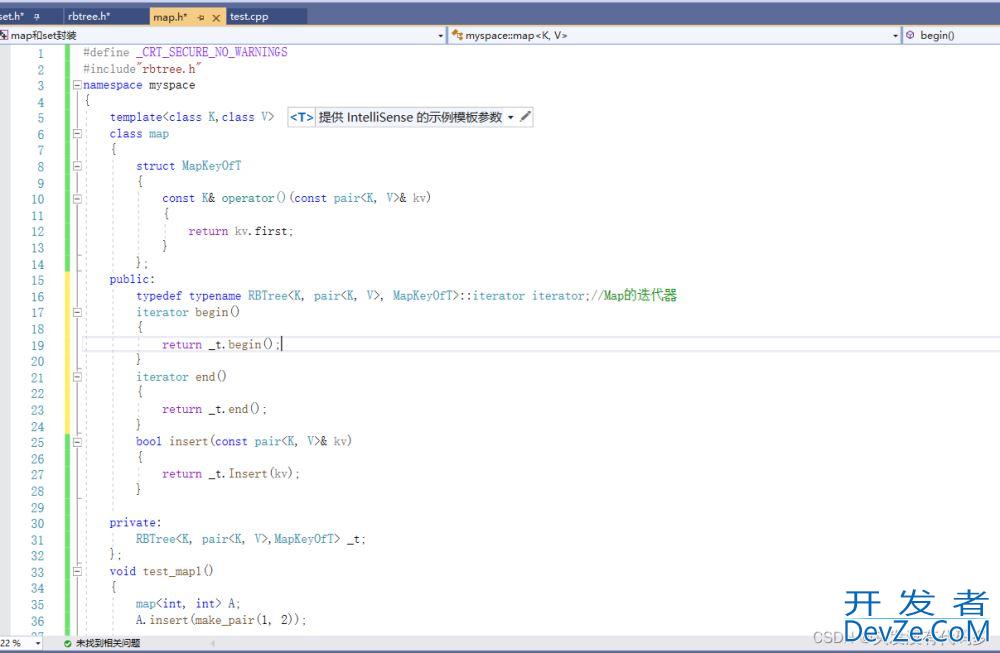
begin和end
template<class K, class T, class KeyOfT>
struct RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef __RBTreeIterator<T, T&, T*> iterator;
iterator begin()
{
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);
}
iterator end()
{
return iterator(nullptr);
}
};
begin是找最左边的节点,这里的_root是红黑树的根节点,end是最后一个节点的下一个位置就是空。
++和--
这里++和--是按照中序进行的
这里访问顺序是左根右
1.如果右子树不为空,++就是找右子树中序的第一个(最左节点)
2.右子树是空,++找孩子不是父亲右的那个父亲
第二句话理解,这里7访问完,父亲是6,7是6右子树,更新cur,parent,8是parent,6是cur,cur不是parent右子树。所以下一个节点是8
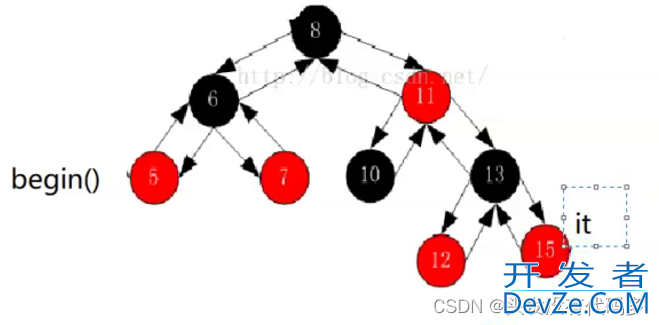
--是反向左子树
右根左
1.如果左子树不为空,我们就访问它的最右节点
2.如果为空,访问孩子不是父亲的左的父亲
Self& operator++()
{
if (_node->_right)
{
// 下一个就是右子树的最左节点
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left;
}
else
{
// 找祖先里面孩子不是祖先的右的那个
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_right)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
if (_node->_left)
{
// 下一个是左子树的最右节点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = right;
}
else
{
// 孩子不是父亲的左的那个祖先
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_left)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
operator[]
[]的实现要改造一个迭代器
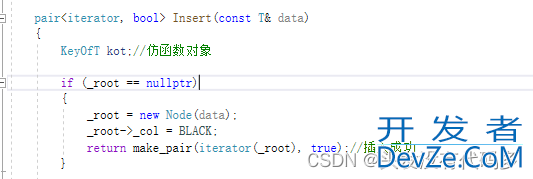
map和set的insert也做修改
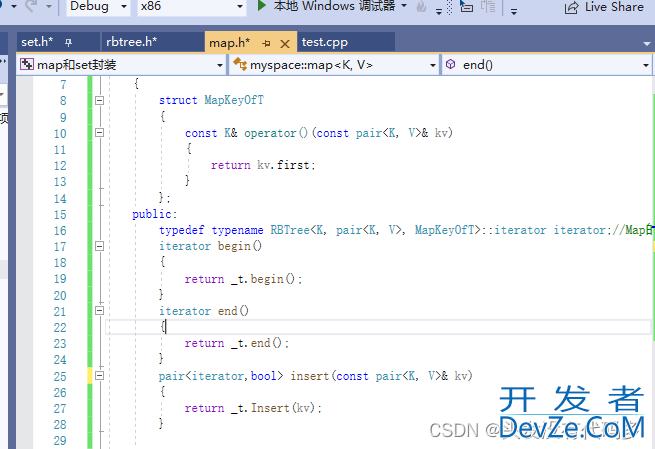
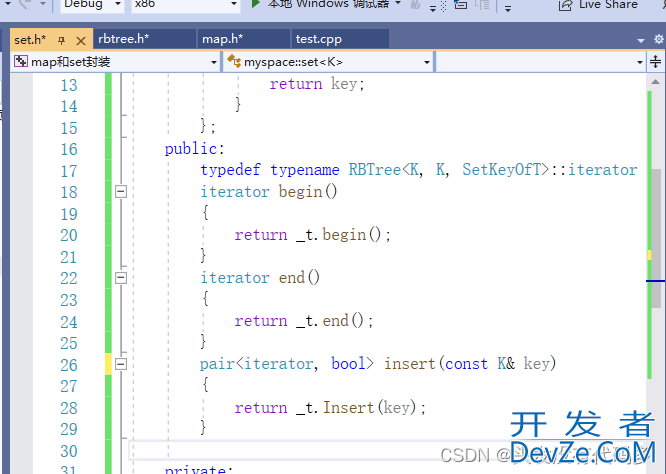
只有map有[],我们不需要在红黑树里面实现[],单独给map实现即可

ret.first是迭代器,->second是KV的value
Map中使用方括号访问键对应的值map[key]时:
- 若该key存在,则访问取得value值;
- 若该key不存在,访问仍然成功,取得value对象默认构造的值。具体如下:用 []访问,但key不存在时,C++会利用该key及默认构造的value,组成{key,value}对,插入到map中。value为 string对象,则构造空串;value为int对象,构造为android0。
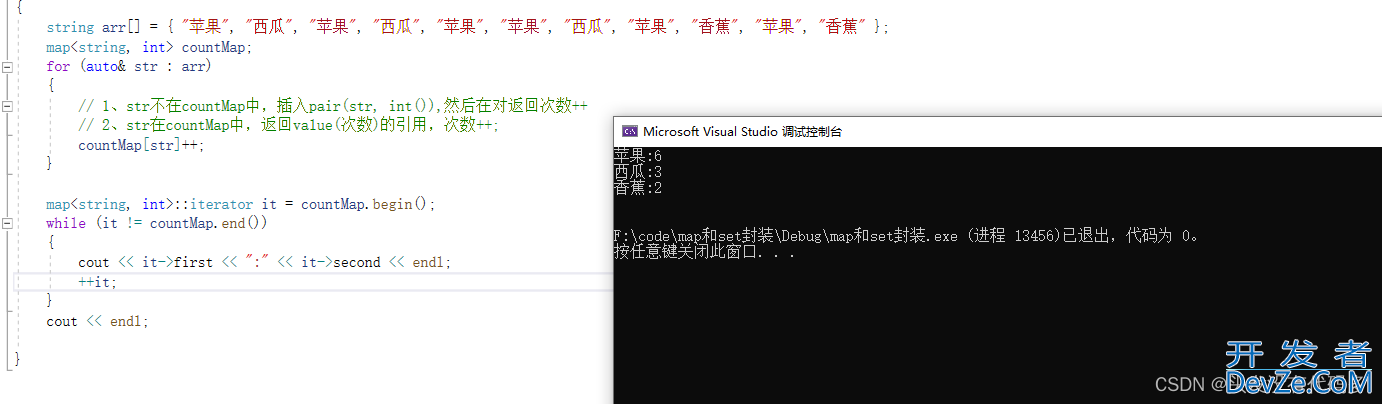
范围for也可以使用
完整代码
set.h
#include"rbtree.h"
namespace myspace
{
template<class K>
class set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K, K, SetKeyOfT&gpythont;::iterator iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<iterator, bool> insert(const K& key)
{
return _t.Insert(key);
}
private:
RBTree<K, K, SetKeyOfT> _t;
};
void test_set()
{
set<int> s;
set<int>::iterator it = s.begin();
while (it != s.end())
{
cout << *it << " ";
++it;
}
cout << endl;
s.insert(3);
s.insert(2);
s.insert(1);
s.insert(5);
s.insert(3);
s.insert(6);
s.insert(4);
s.insert(9);
s.insert(7);
it = s.begin();
while (it != s.end())
{
cout << *it << " ";
++it;
}
cout << endl;
}
}
map.h
#include"rbtree.h"
#pragma once
namespace myspace
{
template<class K, class V>
class map
{
struct MapKeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<iterator, bool> insert(const pair<K, V>& kv)
{
return _t.Insert(kv);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
return ret.first->second;
}
private:
RBTree<K, pair<K, V>, MapKeyOfT> _t;
};
void test_map()
{
string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
map<string, int> countMa开发者_Go开发p;
for (auto& str : arr)
{
// 1、str不在countMap中,插入pair(str, int()),然后在对返回次数++
// 2、str在countMap中,返回value(次数)的引用,次数++;
countMap[str]++;
}
map<string, int>::iterator it = countMap.begin();
while (it != countMap.end())
{
cout << it->first << ":" << it->second << endl;
++it;
}
for (auto& kv : countMap)
{
cout << kv.first << ":" << kv.second << endl;
}
}
}
rbtree.h
enum Colour
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Colour _col;
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
{}
};
template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef __RBTreeIterator<T, Ref, Ptr> Self;
Node* _node;
__RBTreeIterator(Node* node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator!=(const Self& s) const
{
return _node != s._node;
}
bool operator==(const Self& s) const
{
return _node == s._node;
}
Self& operator++()
{
if (_node->_right)
{
// 下一个就是右子树的最左节点
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left;
}
else
{
// 找祖先里面孩子不是祖先的右的那个
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_right)
{
cur = cur->_parent;
parent = parent-php>_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
if (_node->_left)
{
// 下一个是左子树的最右节点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = right;
}
else
{
// 孩子不是父亲的左的那个祖先
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_left)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
};
template<class K, class T, class KeyOfT>
struct RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef __RBTreeIterator<T, T&, T*> iterator;
iterator begin()
{
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);
}
iterator end()
{
return iterator(nullptr);
}
pair<iterator, bool> Insert(const T& data)
{
KeyOfT kot;
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(iterator(_root), true);
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(iterator(cur), false);
}
}
cur = new Node(data);
Node* newnode = cur;
cur->_col = RED;
if (kot(parent->_data) < kot(data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == RED)
{
Node* grandfater = parent->_parent;
assert(grandfater);
assert(grandfater->_col == BLACK);
// 关键看叔叔
if (parent == grandfater->_left)
{
Node* uncle = grandfater->_right;
// 情况一 : uncle存在且为红,变色+继续往上处理
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfater->_col = RED;
// 继续往上处理
cur = grandfater;
parent = cur->_parent;
}// 情况二+三:uncle不存在 + 存在且为黑
else
{
// 情况二:右单旋+变色
// g
// p u
// c
if (cur == parent->_left)
{
RotateR(grandfater);
parent->_col = BLACK;
grandfater->_col = RED;
}
else
{
// 情况三:左右单旋+变色
// g
// p u
// c
RotateL(parent);
RotateR(grandfater);
cur->_col = BLACK;
grandfater->_col = RED;
}
break;
}
}
else // (parent == grandfater->_right)
{
Node* uncle = grandfater->_left;
// 情况一
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfater->_col = RED;
// 继续往上处理
cur = grandfater;
parent = cur->_parent;
}
else
{
// 情况二:左单旋+变色
// g
// u p
// c
if (cur == parent->_right)
{
RotateL(grandfater);
parent->_col = BLACK;
grandfater->_col = RED;
}
else
{
// 情况三:右左单旋+变色
// g
// u p
// c
RotateR(parent);
RotateL(grandfater);
cur->_col = BLACK;
grandfater->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return make_pair(iterator(newnode), true);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalance()
{
if (_root == nullptr)
{
return true;
}
if (_root->_col == RED)
{
cout << "根节点不是黑色" << endl;
return false;
}
// 黑色节点数量基准值
int benchmark = 0;
/*Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
++benchmark;
cur = cur->_left;
}*/
return PrevCheck(_root, 0, benchmark);
}
private:
bool PrevCheck(Node* root, int blackNum, int& benchmark)
{
if (root == nullptr)
{
/编程/cout << blackNum << endl;
//return;
if (benchmark == 0)
{
benchmark = blackNum;
return true;
}
if (blackNum != benchmark)
{
cout << "某条黑色节点的数量不相等" << endl;
return false;
}
else
{
return true;
}
}
if (root->_col == BLACK)
{
++blackNum;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "存在连续的红色节点" << endl;
return false;
}
return PrevCheck(root->_left, blackNum, benchmark)
&& PrevCheck(root->_right, blackNum, benchmark);
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
Node* ppNode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (_root == parent)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
}
private:
Node* _root = nullptr;
};
总结
到此这篇关于C++中map和set封装实现的文章就介绍到这了,更多相关C++ map和set封装内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!

 加载中,请稍侯......
加载中,请稍侯......
精彩评论