使用seaborn绘制强化学习中的图片问题_开发_开发者

seaborn绘制强化学习中的图片

seaborn可以说是matplotlib的升级版，使用seaborn绘制折线图时参数数据可以传递ndarray或者pandas，方便又好看！

本篇用绘制强化学习中的rewards举例，实际上也可以用来机器学习中的loss曲线，原理类似。

从一个简单示例开始

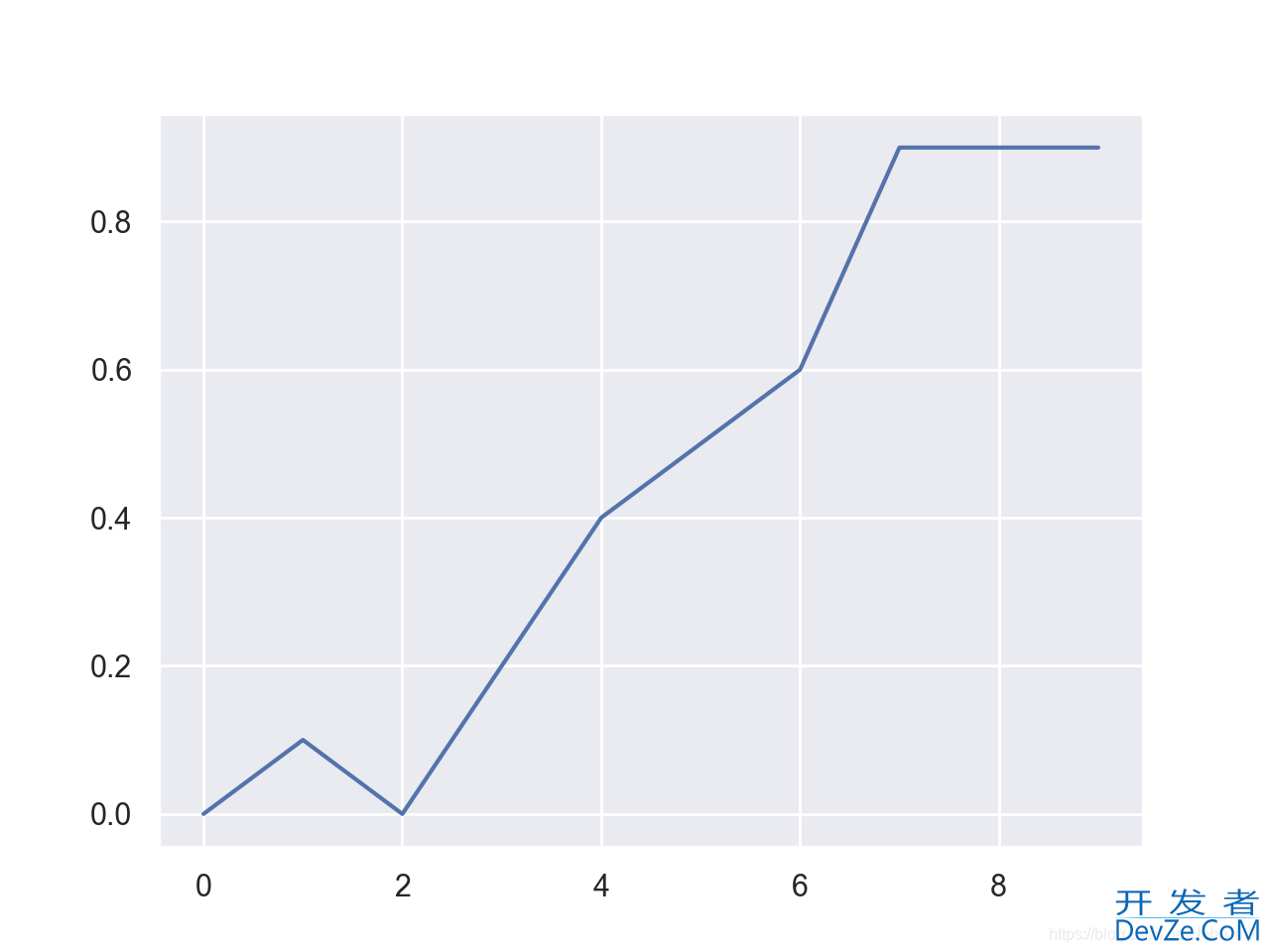
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns # 导入模块
sns.set() # 设置美化参数，一般默认就好

rewards = np.array([0, 0.1,0,0.2,0.4,0.5,0.6,0.9,0.9,0.9])
plt.plot(rewards)
plt.show()

如上首先导入seaborn模块，并设置美化参数(aesthetic parameters)sns.set()，使用matplotlib.pyplot as plt就可以绘制一个基本的图像：

使用seaborn绘制强化学习中的图片问题

使用sns.lineplot或者sns.relplot

实际上relplot包含lineplot和scatterplot，并通过kind传参可以转换为lineplot，

relplot(kind="line")等价于lineplot
relplot(kind="scatter")等价于scatterplot

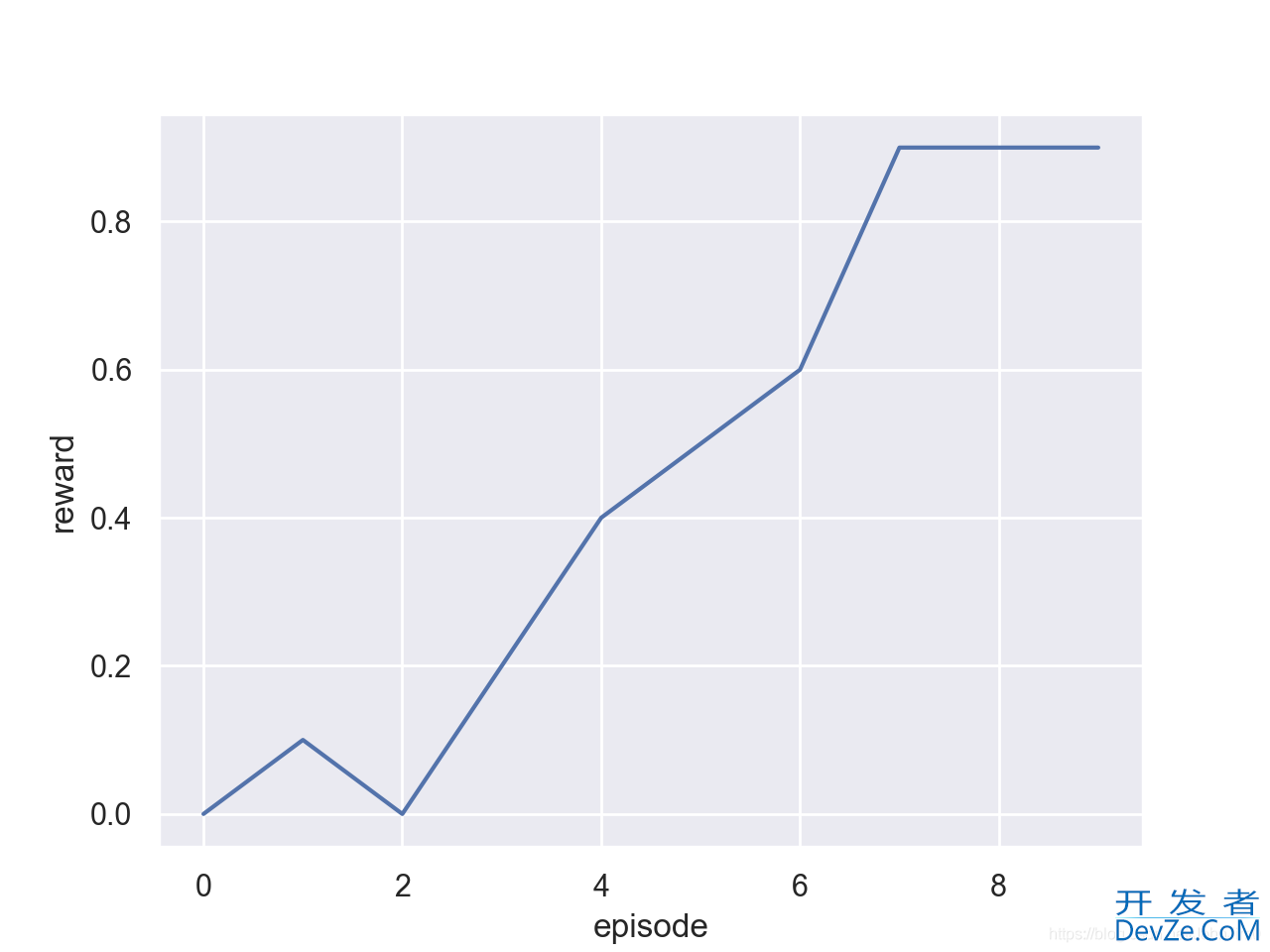
然后再进行适当的调整并加上x，y轴的label，如下：

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns; sns.set() # 因为sns.set()一般不用改，可以在导入模块时顺便设置好

rewards = np.array([0, 0.1,0,0.2,0.4,0.5,0.6,0.9,0.9,0.9])
sns.lineplot(x=range(len(rewards)),y=rewards)
# sns.relplot(x=range(len(rewards)),y=rewards,kind="line") # 与上面一行等价
plt.xlabel("episode")
plt.ylabel("reward")
plt.showphp()

最后呈现效果如下：

使用seaborn绘制强化学习中的图片问题

绘制rewards聚合图

当我们对同一实验作出多次得到一组rewards时，如下：

rewards1 = np.array([0, 0.1,0,0.2,0.4,0.5,0.6,0.9,0.9,0.9])
rewards2 = np.array([0, 0,0.1,0.4,0.5,0.5,0.55,0.8,0.9,1])
rewards=np.vstack((rewards1,rewards2)) # 合并成二维数组

我们希望绘制出聚合图，但是sns.lineplot无法输入一维以上的数据，我们可以将它们全部转为一维，虽然有些难看：

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns; sns.set() # 因为sns.set()一般不用改，可以在导入模块时顺便设置好

rewards1 = np.array([0, 0.1,0,0.2,0.4,0.5,0.6,0.9,0.9,0.9])
rewards2 = np.array([0, 0,0.1,0.4,0.5,0.5,0.55,0.8,0.9,1])
rewards=np.concatenate((rewards1,rewards2)) # 合并数组
episode1=range(len(rewards1))
episode2=range(len(rewards2))
episode=np.concatenate((episode1,episode2))
sns.lineplot(x=episode,y=rewards)
plt.xlabel("episode")
plt.ylabel("reward")
plt.show()

结果如图：

使用seaborn绘制强化学习中的图片问题

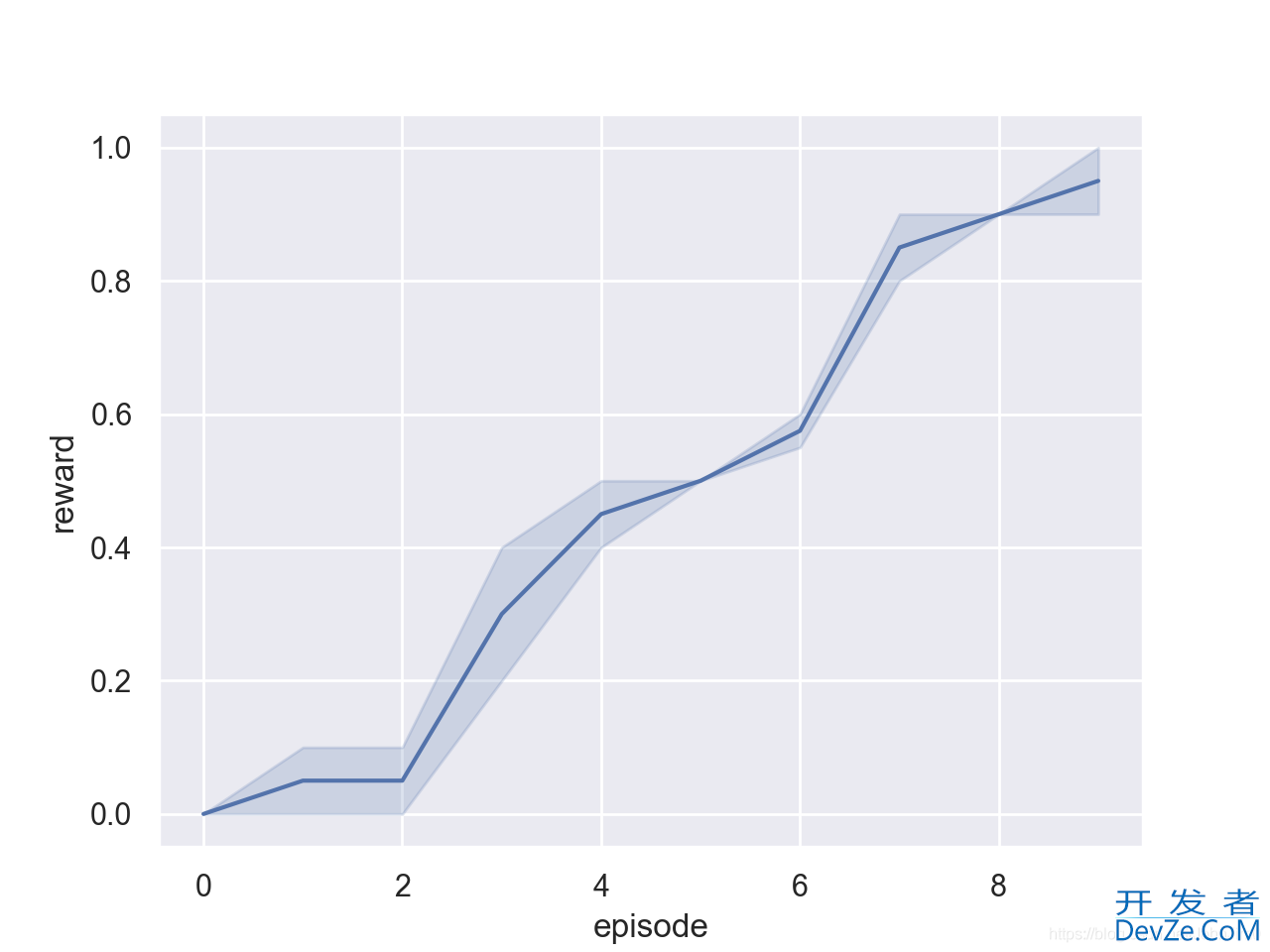
绘制出了带聚合阴影的图，实际上实际部分是seaborn默认对同一x轴的多个y值即rewards做了均值，阴影部分表示多组rewards的范围，可以使用sns.lineplot(x=episode,y=rewards,ci=None)去掉。

使用pandas传参

上面都是用ndarray传参，这样一方面免不了与matplotlib.pyplot混杂的成分比如plt.xlabel，另外绘制rewardandroids聚合图，也比较麻烦。

既然使用pandas传参，就需要先把array转成DataFrame形式，如下：

import numpy as np
import pandas as pd
rewards1 = np.array([0, 0.1,0,0.2,0.4,0.5,0.6,0.9,0.9,0.9])
rewards2 = np.array([0, 0,0.1,0.4,0.5,0.5,0.55,0.8,0.9,1])
rewards=np.vstack((rewards1,rewards2)) # 合并数组
df = pd开发者_JAVA开发.DataFrame(rewards).melt(var_name='episode',value_name='reward') # 推荐这种转换方法
print(df)

推荐上述转化方法，这样无论rewards多少维都不影响最终的绘图方式，其中melt方法将所有维合并成一列，var_name='episode',value_name='reward'则更改对应的列名，转化结果如下：

episode reward
0 0 0.0
1 0 0.1
2 0 0.0
3 0 0.2
4 0 0.4
5 0 0.5
6 0 0.6
7 0 &nbjavascriptsp; 0.9
8 0 0.9
9 0 0.9

下面完整绘图：

import seaborn as sns;sns.set()
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

import pandas as pd
rewards1 = np.array([0, 0.1,0,0.2,0.4,0.5,0.6,0.9,0.9,0.9])
rewards2 = np.array([0, 0,0.1,0.4,0.5,0.5,0.55,0.8,0.9,1])
rewards=np.vstack((rewards1,rewards2)) # 合并数组
df = pd.DataFrame(rewards).melt(var_name='episode',value_name='reward')

sns.lineplot(x="episode", y="reward", data=df)
plt.show()

注意这里的x,y不再传入数组，而是传入DataFrame中对应的列名，类似于python字典中的键

结果如下：

使用seaborn绘制强化学习中的图片问题

牛刀小试

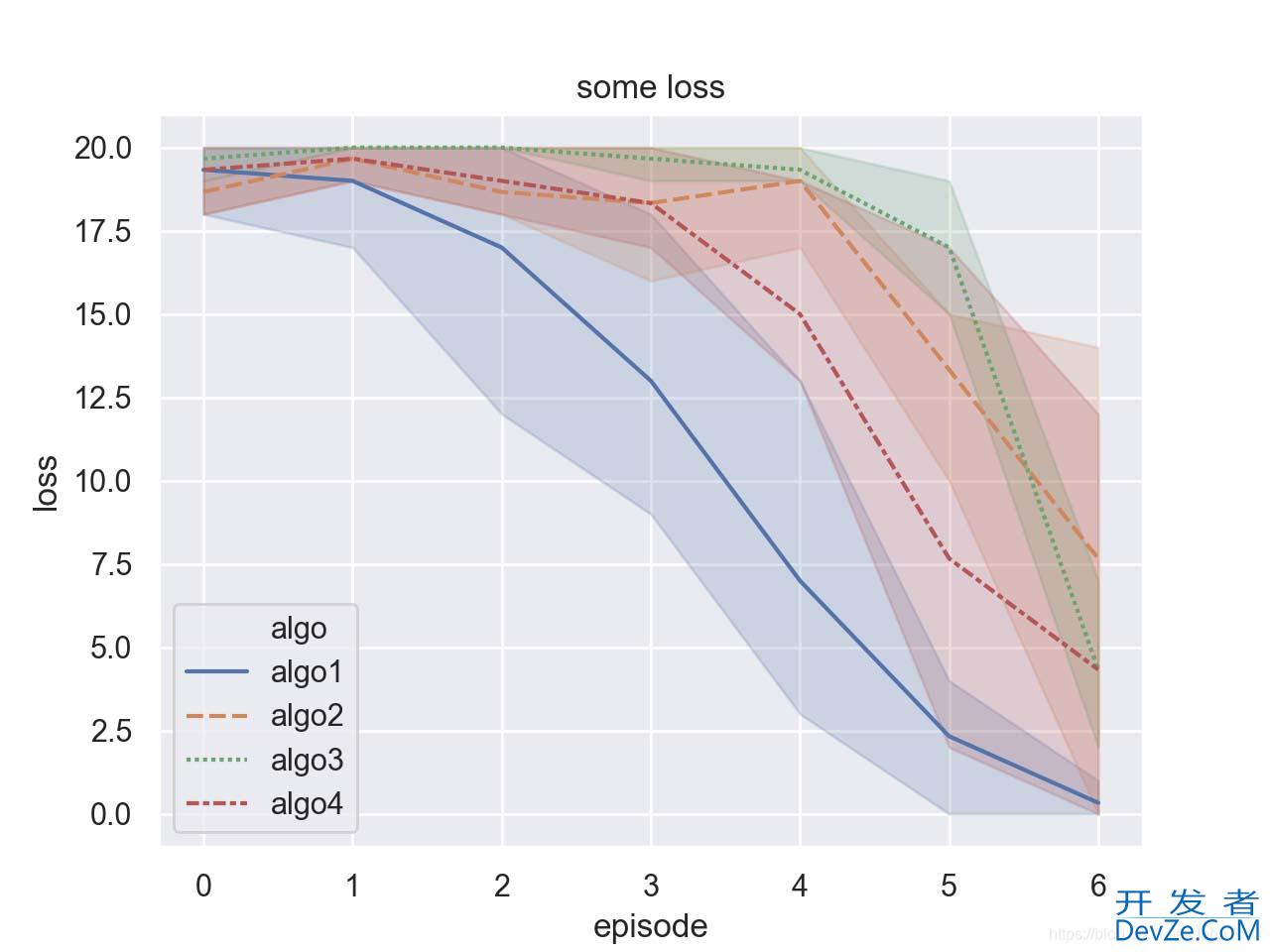
最后绘制一个更为复杂的可以用于paper的绘制方法：

import seaborn as sns; sns.set()
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

def get_data():
    '''获取数据
    '''
    basecond = np.array([[18, 20, 19, 18, 13, 4, 1],[20, 17, 12, 9, 3, 0, 0],[20, 20, 20, 12, 5, 3, 0]])
    cond1 = np.array([[18, 19, 18, 19, 20, 15, 14],[19, 20, 18, 16, 20, 15, 9],[19, 20, 20, 20, 17, 10, 0]]) 
    cond2 = np.array([[20, 20, 20, 20, 19, 17, 4],[20, 20, 20, 20, 20, 19, 7],[19, 20, 20, 19, 19, 15, 2]]) 
    cond3 = np.array([[20, 20, 20, 20, 19, 17, 12],[18, 20, 19, 18, 13, 4, 1], [20, 19, 18, 17, 13, 2, 0]])    
    retuandroidrn basecond, cond1, cojsnd2, cond3
    
data = get_data()
label = ['algo1', 'algo2', 'algo3', 'algo4']
df=[]
for i in range(len(data)):
    df.append(pd.DataFrame(data[i]).melt(var_name='episode',value_name='loss'))
    df[i]['algo']= label[i] 

df=pd.concat(df) # 合并
sns.lineplot(x="episode", y="loss", hue="algo", style="algo",data=df)
plt.title("some loss")
plt.show()

结果如下：

使用seaborn绘制强化学习中的图片问题