C++回溯算法之深度优先搜索详细介绍_开发_开发者

一、前言

本文介绍了经典搜索算法：深度优先搜索（DFS）

两个小故事：

岳云鹏的相声：孙越的爸爸带他参观家里面的聚宝盆，走到了一个密室门前，密室的门上上了一把锁，孙越的爸爸身上带了一万多把钥匙，他还忘了哪一把钥匙能打开个门了，于是就一把把试，试到了最后一把，门开了。

你叫DFS，在一次校园活动中你认识了三个非常漂亮的女孩，你想和她们进一步发展。于是，你选择了其中一个人，并对她展开了追求，你采用了聊天->约会->表白的恋爱三部曲。但是很不幸，她拒绝了你，于是你添加了第二个女生的微信，同样采取了你常用的三部曲。很不幸，第二个女生也拒绝你了。但是，你没有被困难打倒，于是你添加了第三个女生的微信，依旧是这三部曲，终于，第三个女生答应了你。你的朋友询问你，是如何找到女朋友的？，你答：我采用了DFS对象法

二、基本概念

1.简单介绍

前言中的两个小故事，孙越的爸爸找钥匙开门的过程和DFS小朋友找女朋友都是一个搜索过程。

简而言之，搜索就是尝试问题中所有的可能性，在所有的可能性中找到正确的结果。而深度优先搜索用一句话概括就是：“ 一直往下走，走到最后还是走编程客栈不通，那就换条路再走，直到无路可走。”用一个成语来形容，那就是：“ 不撞南墙不回头。”

2.官方概念

以下是维基百科上的解释：

深度优先搜索算法（英语：Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。这个算法会尽可能深地搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的开发者_JS培训起始节点。这一过python程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。这种算法不会根据图的结构等信息调整执行策略

三、动图分析

DFS会从初始节点出发，按预定的顺序扩展到下一个节点，然后从下一节点出发继续扩展新的节点，不断递归执行这个过程，直到某个节点不能再扩展下一个节点为止。此时，则返回上一个节点重新寻找一个新的扩展节点。如此搜索下去，直到找到目标节点，或者搜索完所有节点为止。

动图：

C++回溯算法之深度优先搜索详细介绍

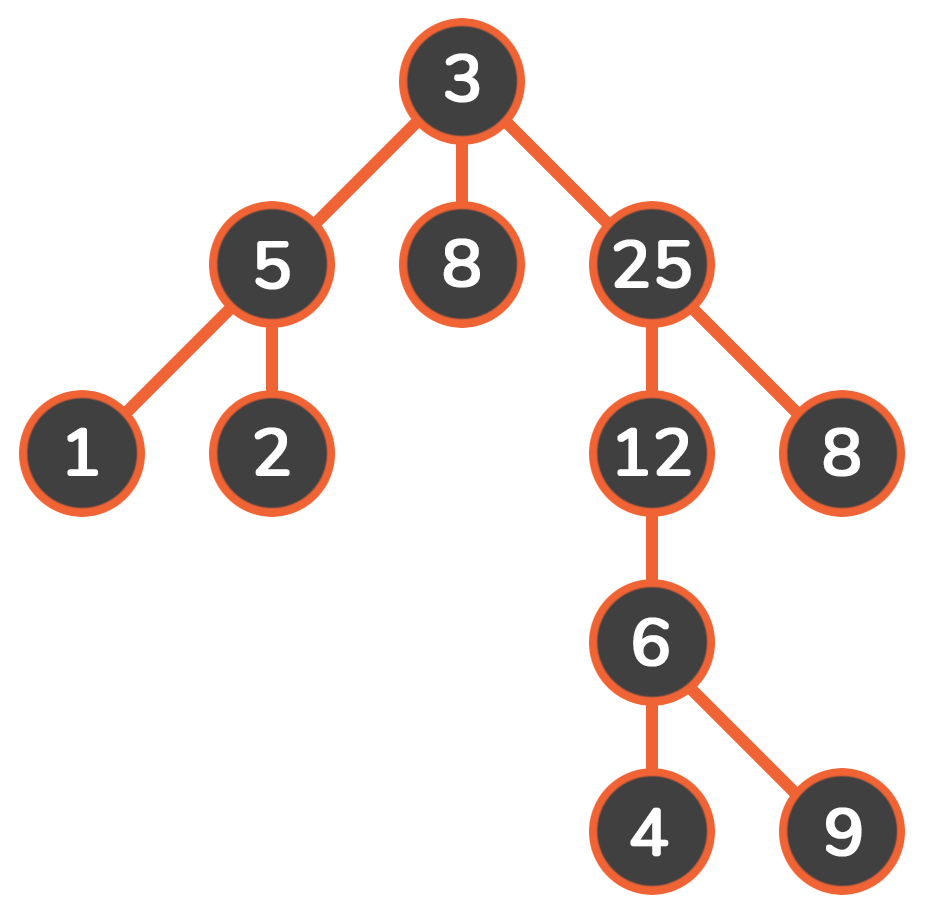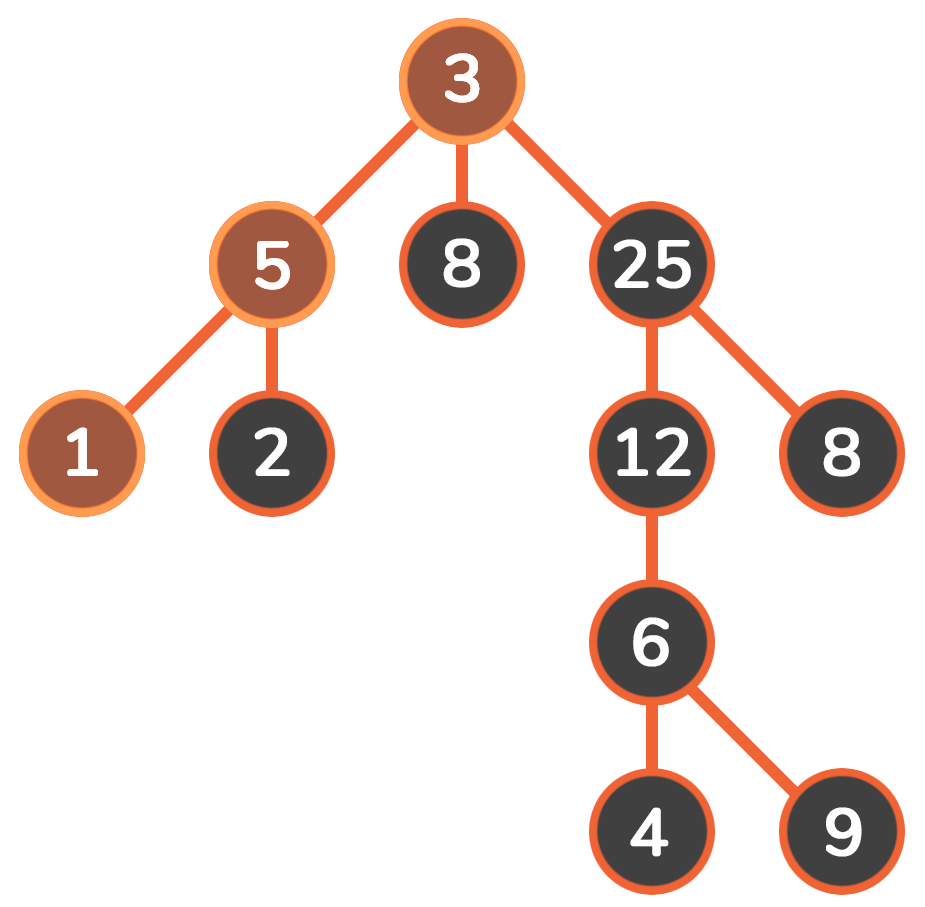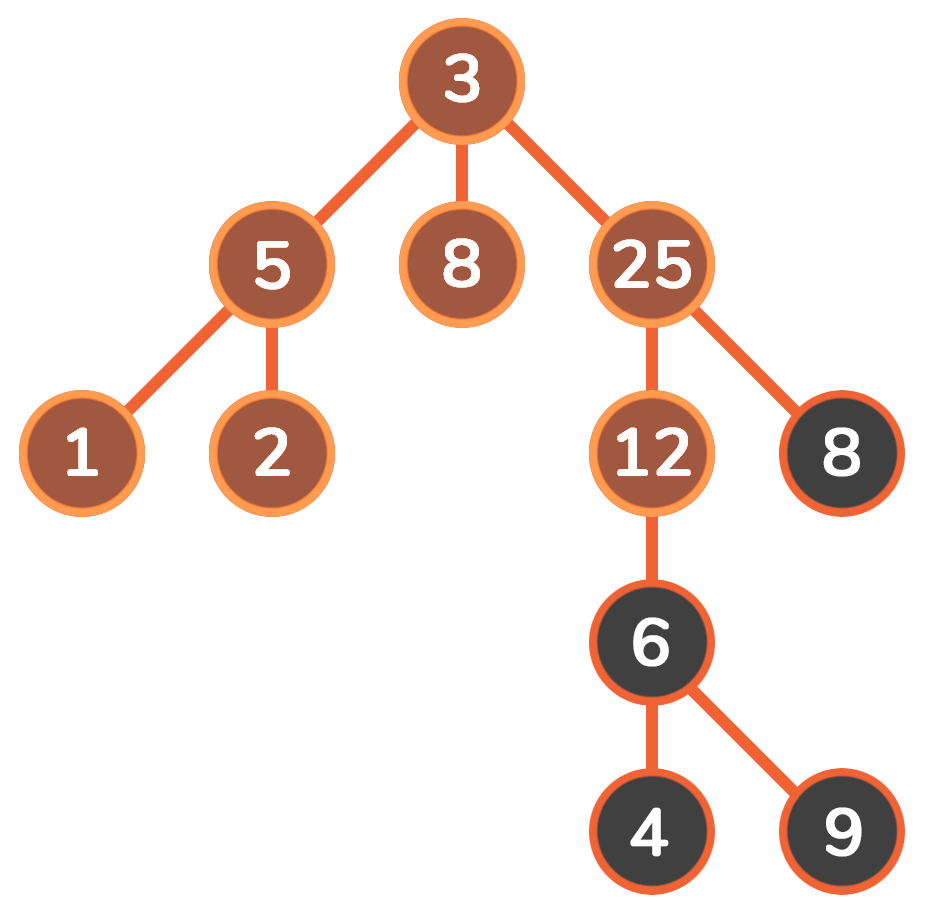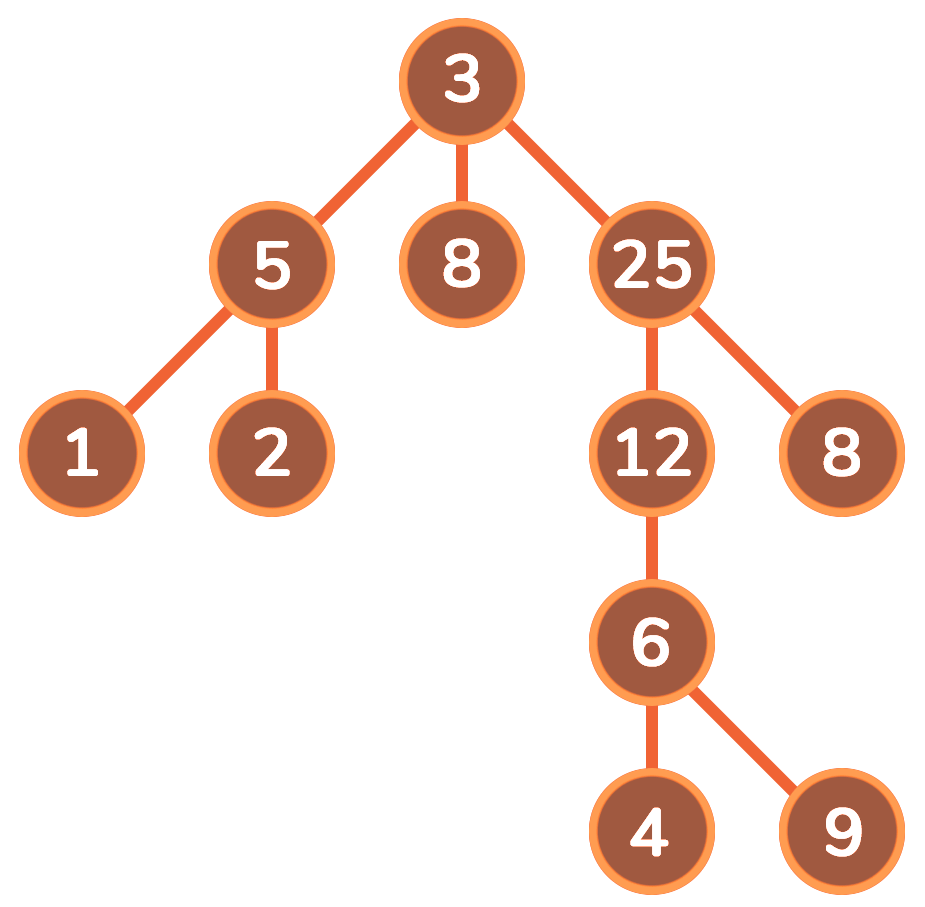
四、模板框架

以下模板来自于大佬Carlwww.devze.com：

void DFS(参数){
    if (终止条件){
        做要做的事
        return ;//退出 
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）)
    	{
    		处理节点;
            DFS(路径，选择列表);
            回溯：回到没用过
        }
    return ;//退出 
}

五、例题分析

组合问题

题干描述

力扣77题：组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。

输入：n = 4, k = 2

输出：

[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

输入：n = 1, k = 1

输出：

[[1]]

思路分析

C++回溯算法之深度优先搜索详细介绍

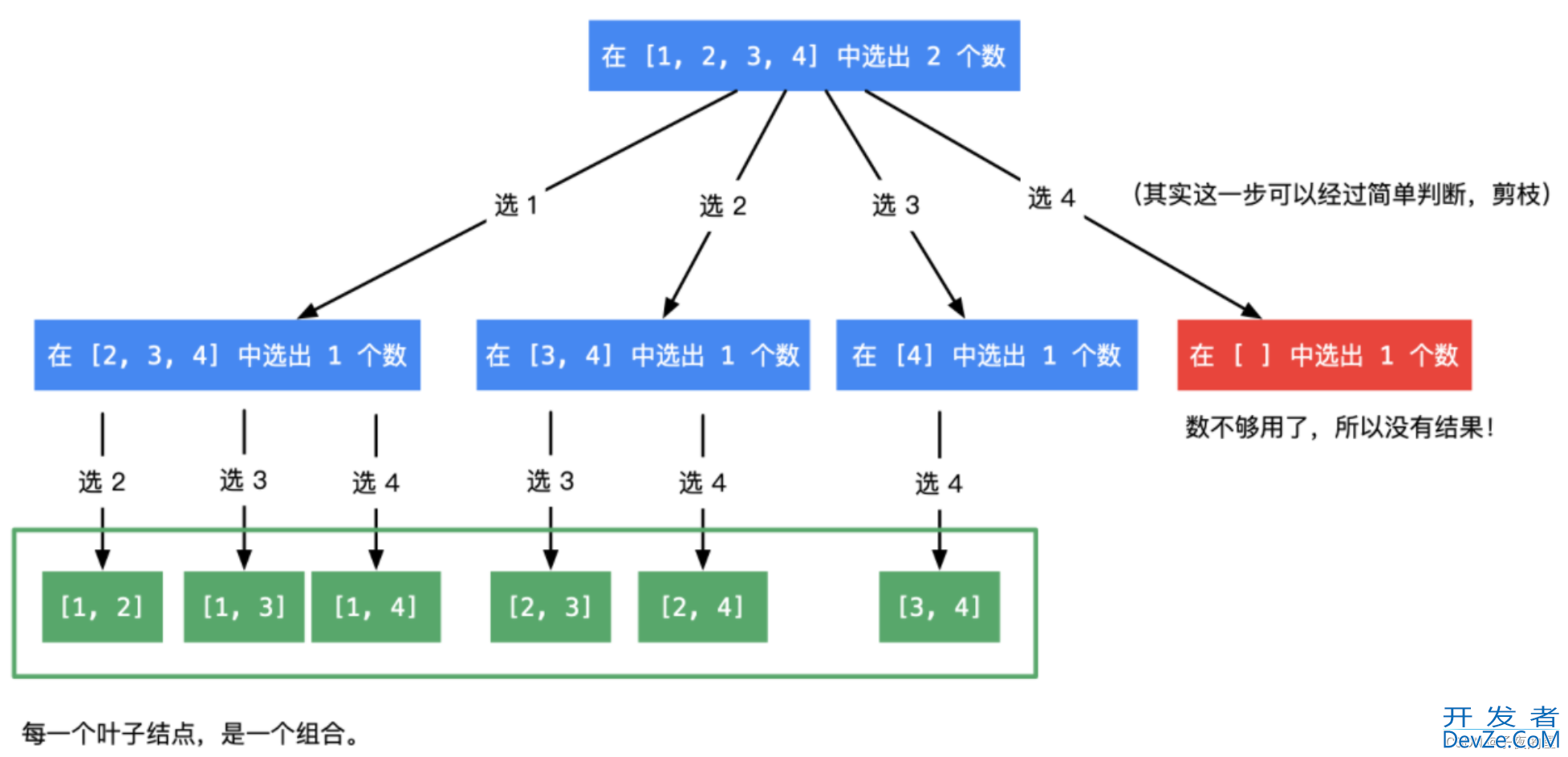
C语言代码：

int* path;
int pathTop;
int** ans;
int ansTop;
void DFS(int n, int k,int startIndex) {
    //当path中元素个数为k个时，我们需要将path数组放编程入ans二维数组中android
    if(pathTop == k) {
        //path数组为我们动态申请，若直接将其地址放入二维数组，path数组中的值会随着我们回溯而逐渐变化
        //因此创建新的数组存储path中的值
        int* temp = (int*)malloc(sizeof(int) * k);
        int i;
        for(i = 0; i < k; i++) {
            temp[i] = path[i];
        }
        ans[ansTop++] = temp;
        return ;
    }
    int j;
    for(j = startIndex; j <=n ;j++) {
        //将当前结点放入path数组
        path[pathTop++] = j;
        //进行递归
        DFS(n, k, j + 1);
        //进行回溯，将数组最上层结点弹出
        pathTop--;
    }
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
    //path数组存储符合条件的结果
    path = (int*)malloc(sizeof(int) * k);
    //ans二维数组存储符合条件的结果数组的集合。（数组足够大，避免极端情况）
    ans = (int**)malloc(sizeof(int*) * 10000);
    pathTop = ansTop = 0;
    DFS(n, k, 1);
    //最后的返回大小为ans数组大小
    *returnSize = ansTop;
    //returnColumnSizes数组存储ans二维数组对应下标中一维数组的长度（都为k）
    *returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
    int i;
    for(i = 0; i < *returnSize; i++) {
        (*returnColumnSizes)[i] = k;
    }
    //返回ans二维数组
    return ans;
}

到此这篇关于C++回溯算法之深度优先搜索详细介绍的文章就介绍到这了,更多相关C++深度优先搜索内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！