C++中二叉堆排序详解

目录

• 1. 前言
• 什么是二叉堆？
• 2 堆的数据结构
• 2.1 二叉堆的抽象数据结构
• 2.2 基础 API 实现
• 2.3 上沉算法
• 2.4 下沉算法
• 3. 堆排序
• 4. 后记

1. 前言

什么是二叉堆？

二叉堆是有序的 完全二叉树，在完全二叉树的基础上，二叉堆 提供了有序性特征：

二叉堆 的根结点上的值是整个堆中的最小值或最大值。

当根结点上的值是整个堆结构中的最小值时，此堆称为最小堆。最小堆中，任意节点的值大于父结点的值。

当根结点上的值是整个堆结构中的最大值时，则称堆为最大堆。最大堆中，任意节点的值小于父结点的值。

根据完全二叉树的特性，二叉堆的父结点与子结点之间满足下面的关系：

如果知道了一个结点的位置 i，则其左子结点在 2*i 位置，右子结点在 2*i+1 位置。

Tips： 前提是存在有子结点。

如果知道了一个结点的位置 i，则其父结点在 i除以 2 的位置。

Tips： 根结点没有父结点。

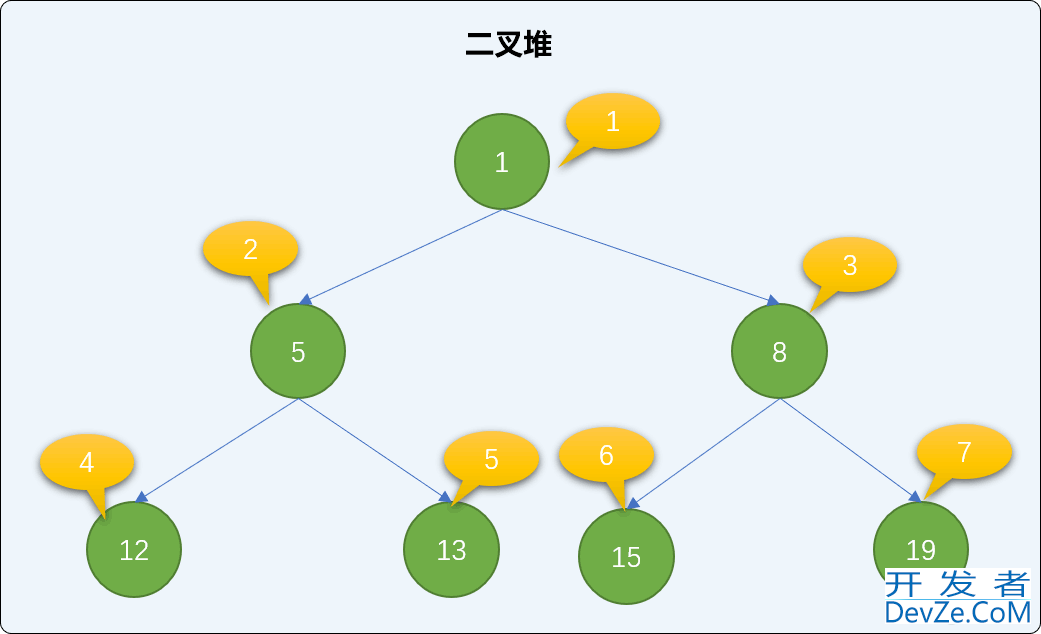
如上图所示：

值为 5 的结点在 2 处，则其左结点 12 的位置应该在 2*2=4 处，而实际情况也是在 4 位置。其右子结点 13 的位置应该在 2*2+1=5 的位置，实际位置也是在 5 位置。

值为 19 的结点现在 7 位置，其父结点的根据公式 7 除 2 等于 3(取整)，应该在 3 处，而实际情况也是在 3 处（位置在 3、 值为编程客栈 8 的结点是其父结点）。

2 堆的数据结构

2.1 二叉堆的抽象数据结构

当谈论某种数据结构的抽象数据结构时，最基本的 API 无非就是增、删、改、查。

二叉堆的基本抽象数据结构：

Heap() ：创建一个新堆。 insert(data)： 向堆中添加新节点（数据）。 getRoot()： 返回最小（大）堆的最小（大）元素。 removeRoot() ：删除根节点。 isEmpty()：判断堆是否为空。 findAll()：查询堆中所有数据。

根据二叉堆的特性，顺序存储应该成为堆的首选方案。

如有数列=[8,5,12,15,19,13,1]，可以先创建一个一维数组。

数组第 0 位置初始为 0，python从第 2 个位置也就是索引号为 1 的地方开始存储堆的数据。如下图，二叉堆中的数据在数组中的对应存储位置。

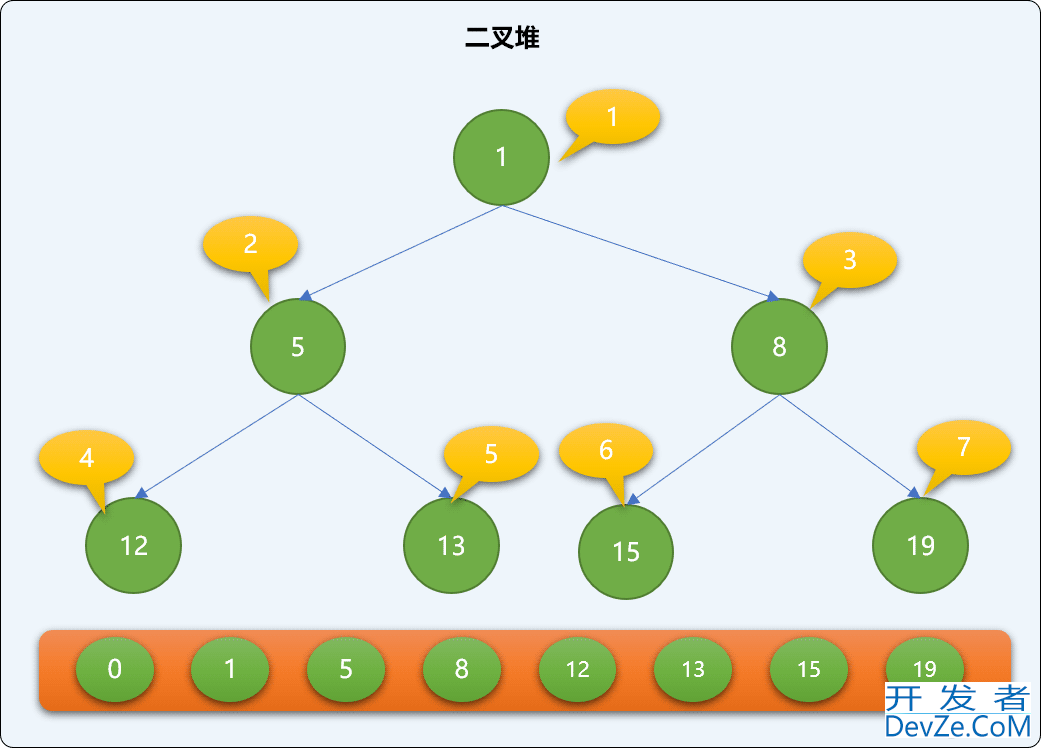
2.2 基础 API 实现

设计一个 Heap 类封装对二叉堆的操作方法，类中方法用来编程客栈实现最小堆。

#include <IOStream>
using namespace std;
/* 
* 堆类 
*/ 
template<typename T>
class Heap{
    private:
    	
    	//数组
    	T heapList[100];
    	//实际大小
		int size=0; 
		
	public:
		
		/*
		*构造函数 
		*/ 
		Heap(){
		} 
		
		/*
		*返回根结点的值 
		*/
		T getRoot();
		
		/*
		*删除根结点 
		*/
		T removeRoot();
    	
    	/*
		*递归删除
		*/
		T removeRoot_();
		void removeRootByRecursion(int parentIdx );
		
		/*
		*初始化根结点 
		*/ 
		void setRoot(T val);
		
		/*
		*添加新结点,返回存储位置 
		*/
		int insert(T  val);
		
		/*
		*堆是否为空 
		*/ 
		bool isEmpty();
    
    	/*
		* 递归插入 
		*/
		int insert_(T  val);
		int insertByRecursion(int  pos);
		
		/*
		*输出所有结点
		*/
		void findAll() {
			for(int i=0; i<=size; i++)
				cout<<this->heapList[i]<<"\t";
			cout<<endl;
		}	 
}; 

Heap 类中的属性详解：

heapList：使用数组存储二叉堆的数据，初始时，列表的开发者_JS教程第 0 位置初始为默认值 0。

Tips： 为什么要设置列表的第 0 位置的默认值为 0？

这个 0 也不是随意指定的，有其特殊数据含义：用来描述根结点的父结点编号或者说根结点没有父结点。

size：用来存储二叉堆中数据的实际个数。

Heap 类中的方法介绍：

isEmpty：检查是不是空堆。逻辑较简单。

/*
*当 size 为 0 时，堆为空 
*/
template<typename T>
bool Heap<T>::isEmpty(){
	return Heap::size==0;
}

setRoot：创建根结点。保证根节点始终存储在列表索引为 1 的位置。

/*
*初始化根结点
*/
template<typename T>
void Heap<T>::setRoot(T val) {
	if( Heap<T>::heapList[1]==0  )
		Heap<T>::heapList[1]=val;
		Heap<T>::size++;
}

getRoot：如果是最大堆，则返回二叉堆的最大值，如果是最小堆，则返回二叉堆的最小值。

/*
*返回根结点
*/
template<typename T>
T Heap<T>::getRoot() {
	if( !Heap<T>::isEmpty  )
		return	Heap<T>::heapList[1];
}

Tips： 使用数组存储二叉堆数据时，根结点始终保存在索引号为 1 的位置。

前面是几个基本方法，现在实现添加新结点，编码之前，先要知道如何在二叉堆中添加新结点：

2.3 上沉算法

添加新结点采用上沉算法。如下演示上沉算法的实现过程。

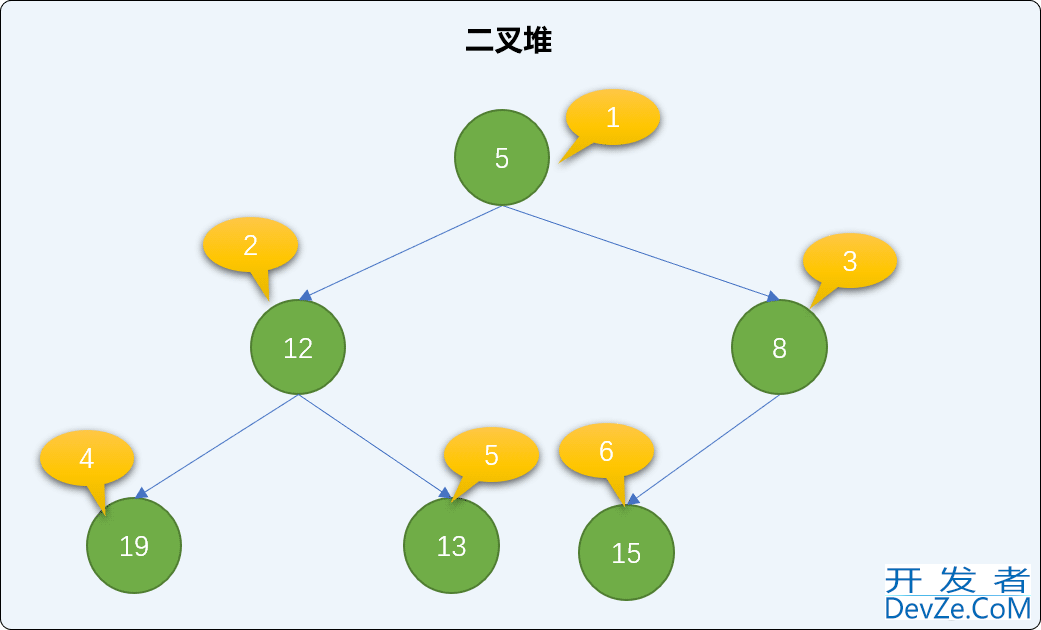
把新结点添加到已有的二叉堆的最后面。如下图，添加值为 4 的新结点，存储至索引号为 7 的位置。

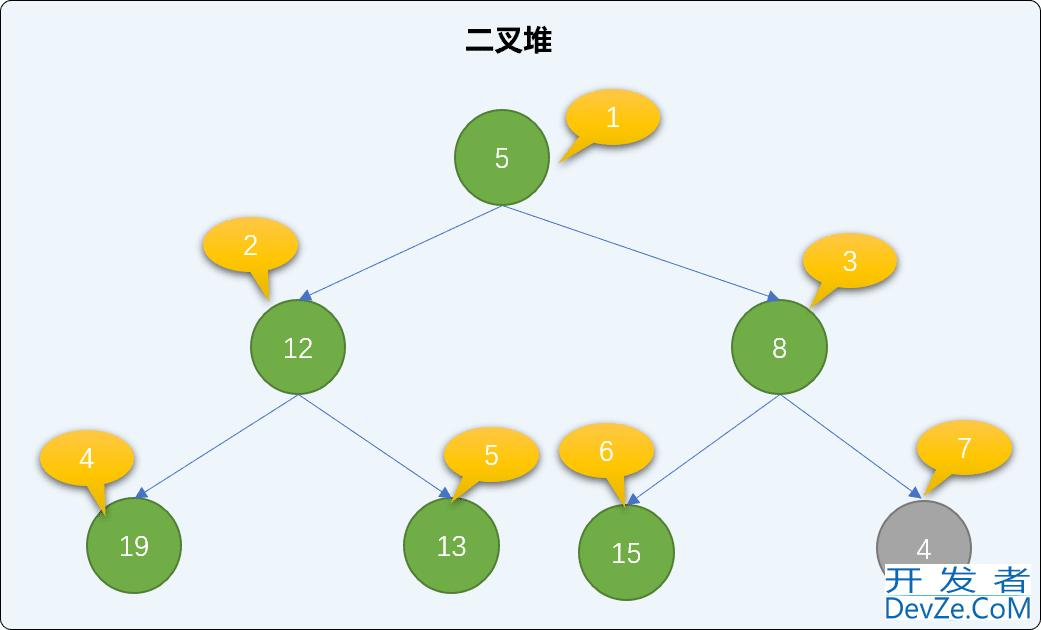
查找新结点的父结点，并与父结点的值比较大小，如果比父结点的值小，则和父结点交换位置。如下图，值为 4 的结点小于值为 8 的父结点，两者交换位置。

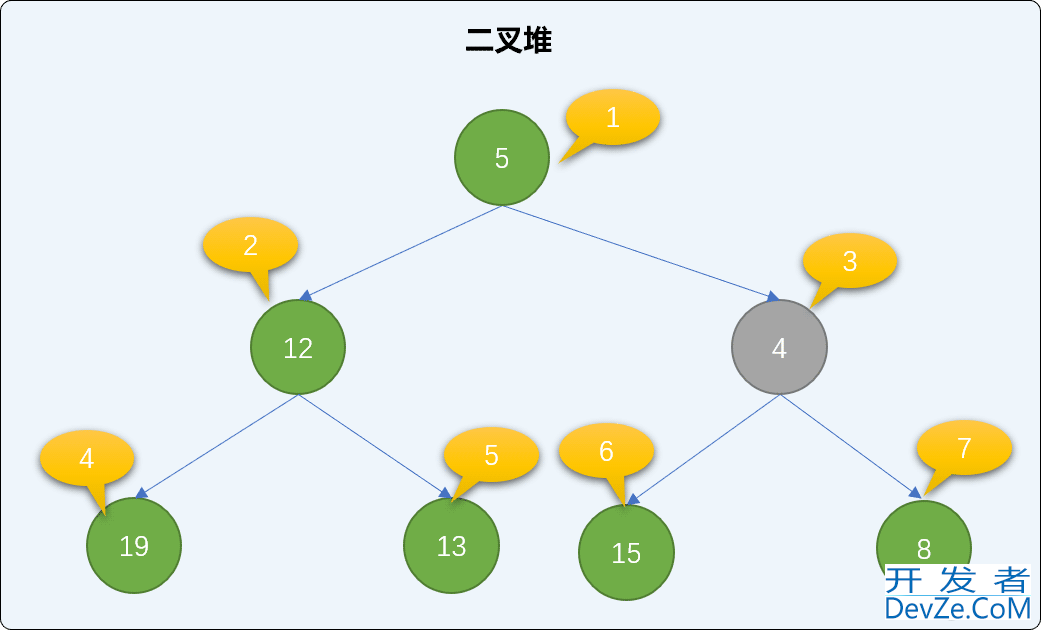
交换后再查询是否存在父结点，如果有，同样比较大小、交换，直到到达根结点或比父结点大为止。值为 4 的结点小于值为 5 的父结点，继续交换。交换后，新结点已经达到了根结点位置，整个添加过程可结束。观察后会发现，遵循此流程添加后，没有破坏二叉堆的有序性。

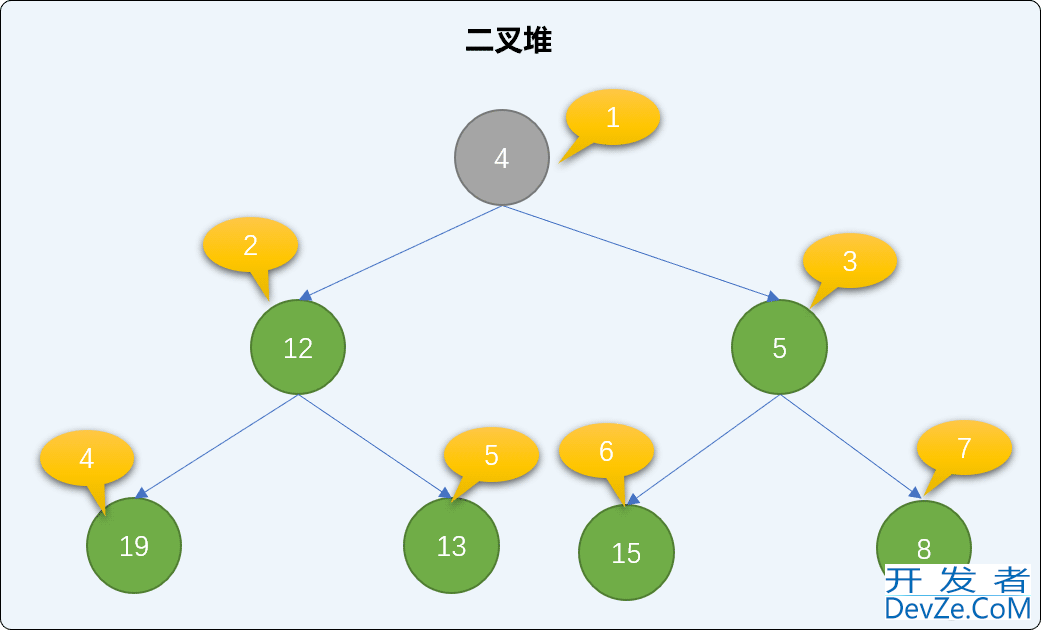
编码实现 insert 方法

/*
*添加新结点
*/
template<typename T>
T Heap<T>::insert(T val) {
	//存储在最后一个位置
	int pos= ++Heap<T>::size;
	Heap<T>::heapList[pos]=val;
	int temp=0;
	//上沉算法
	while(1) {
		//找到父结点位置
		int parentIdx=  pos / 2;
		if(parentIdx==0)
			//出口一，没有父结点
			breaandroidk;
		if( Heap<T>::heapList[pos]>Heap<T>::heapList[parentIdx] )
			//出口二：大于父结点
			break;
		else {
			//和父亲结点交换
			temp=Heap<T>::heapList[pos];
			Heap<T>::heapList[pos]=Heap<T>::heapList[parentIdx];
			Heap<T>::heapList[parentIdx]=temp;
			pos=parentIdx
		}
	}
}

测试向二叉堆中添加数据。

int main(int argc, char** argv) {
	//实例化堆
	Heap<int> heap;
	//初始化根结点
	heap.setRoot(5);
	//检查根结点是否创建成功
	int rootVal=heap.getRoot();
	cout<<"根结点的值："<<rootVal<<endl;
	//添加值为 12和值为  13 的 2个新结点，检查添加新结点后整个二叉堆的有序性是否正确。
	heap.insert(12);
	heap.insert(13);
	cout<<"测试一："<<endl;
	heap.findAll();
	return 0;
}

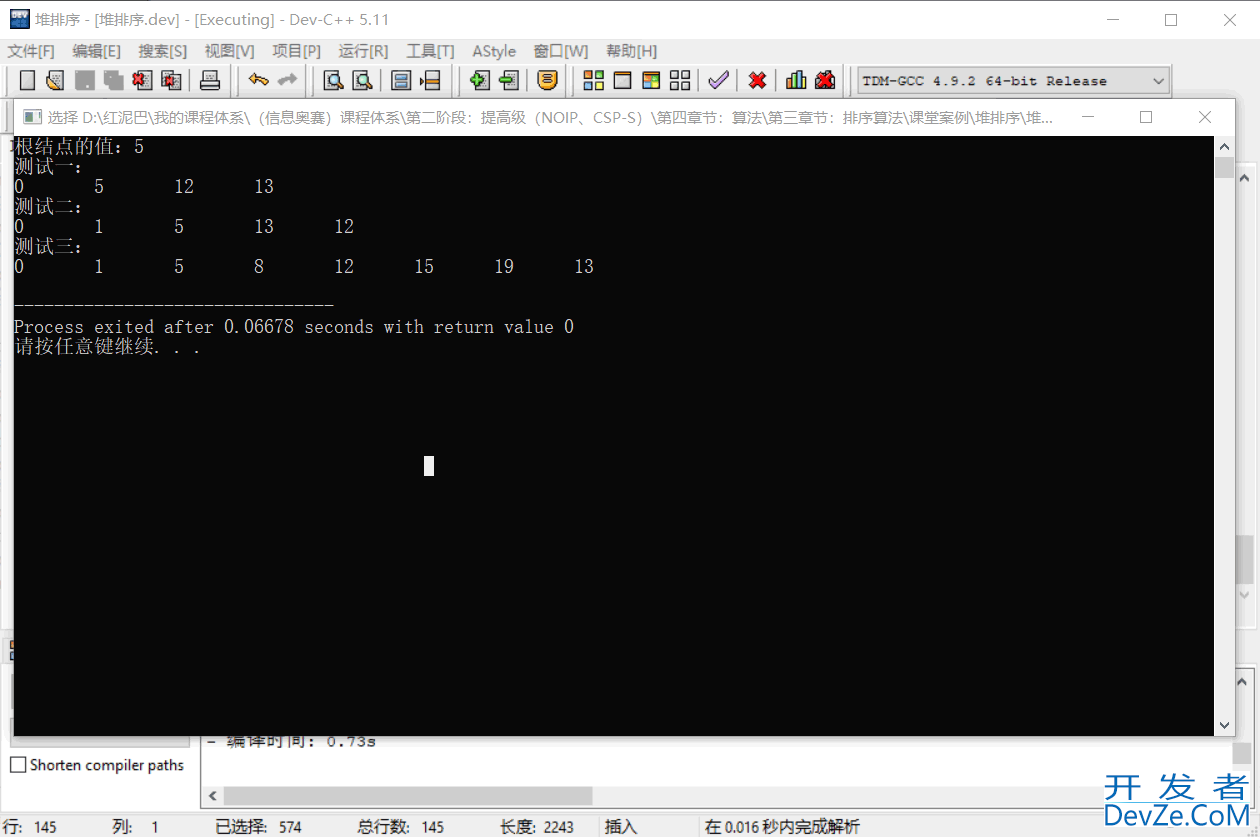
输出结果：

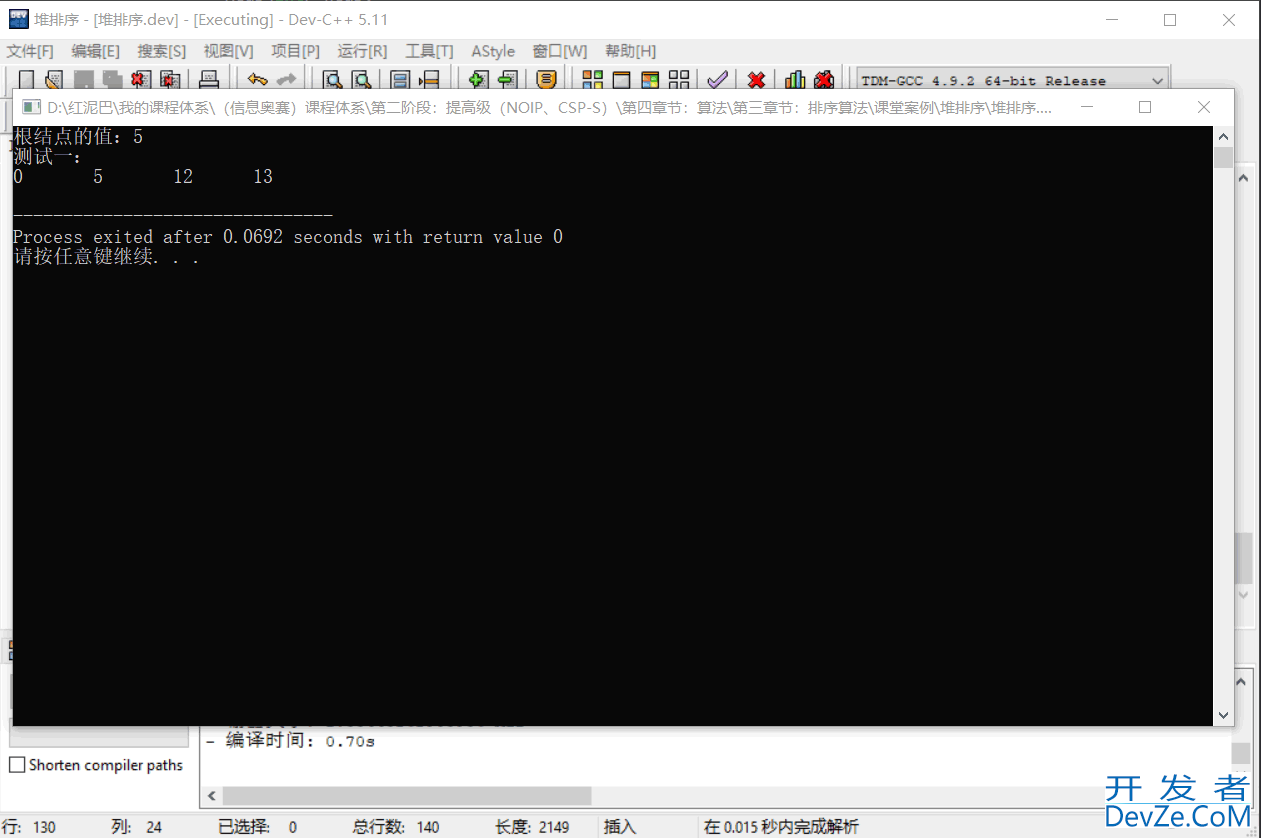
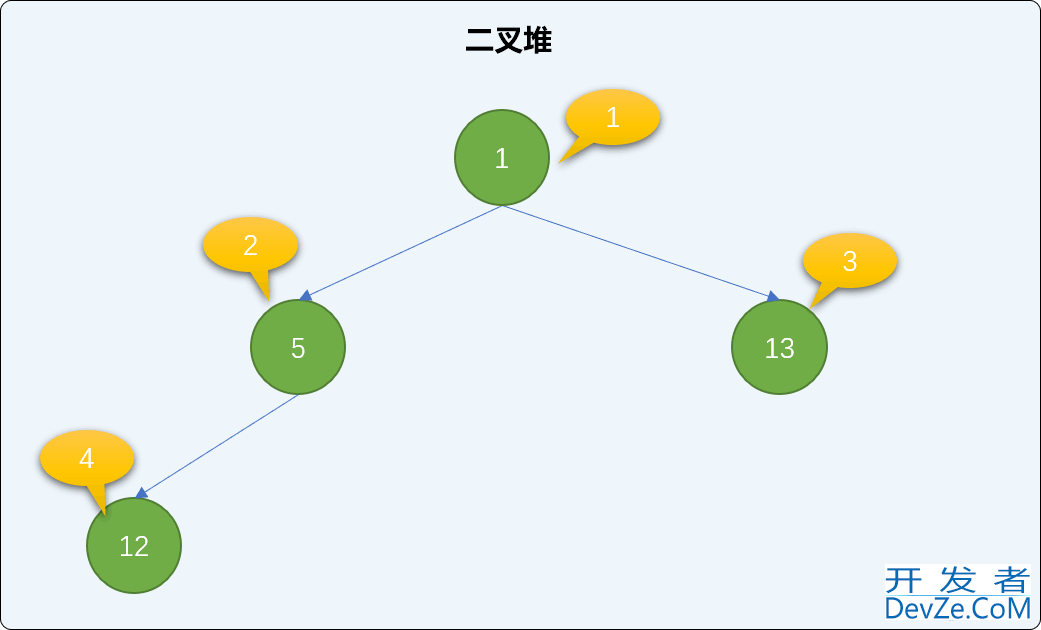
添加值为 1 的新结点，并检查二叉堆的有序性。

int main(int argc, char** argv) {
	//省略……
    //添加值为 1 的结点
	heap.insert(1);
	cout<<"测试二："<<endl;
	heap.findAll();
	return 0;
}

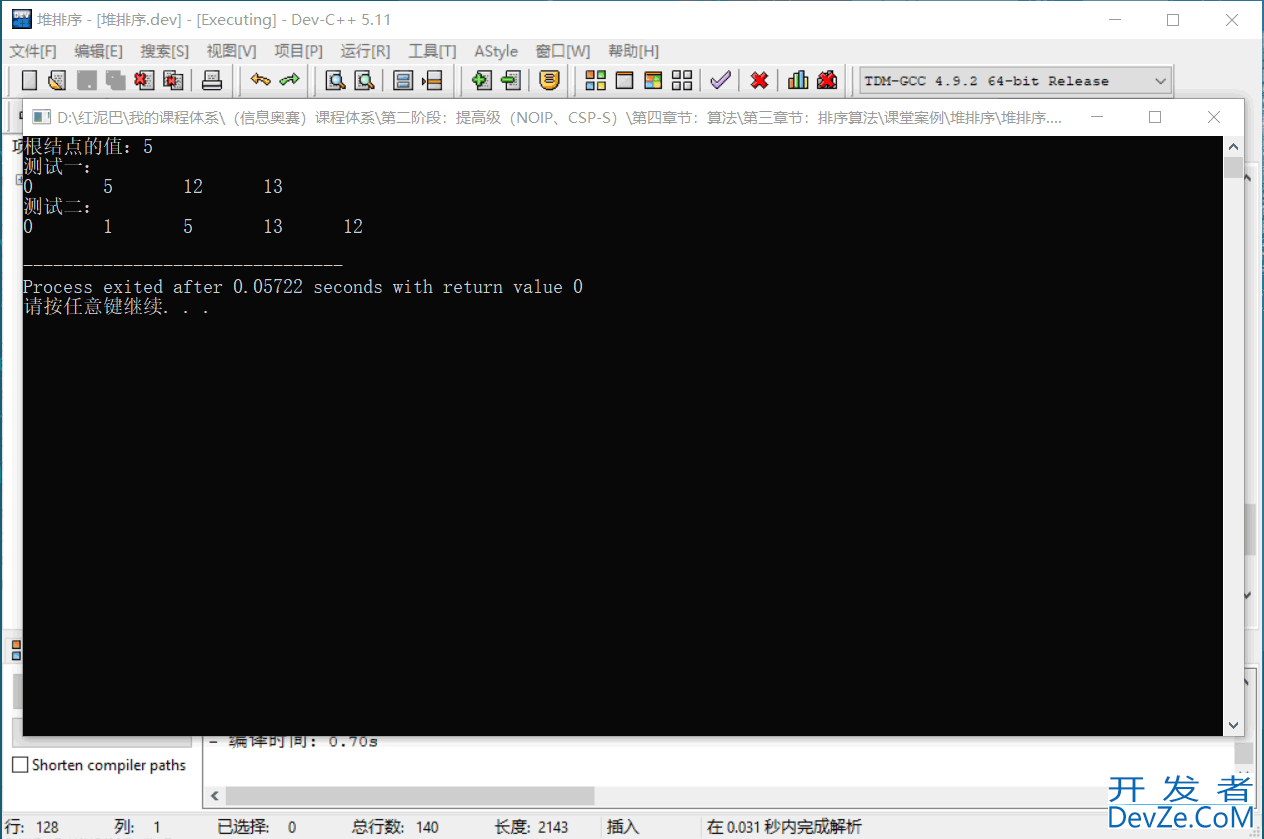
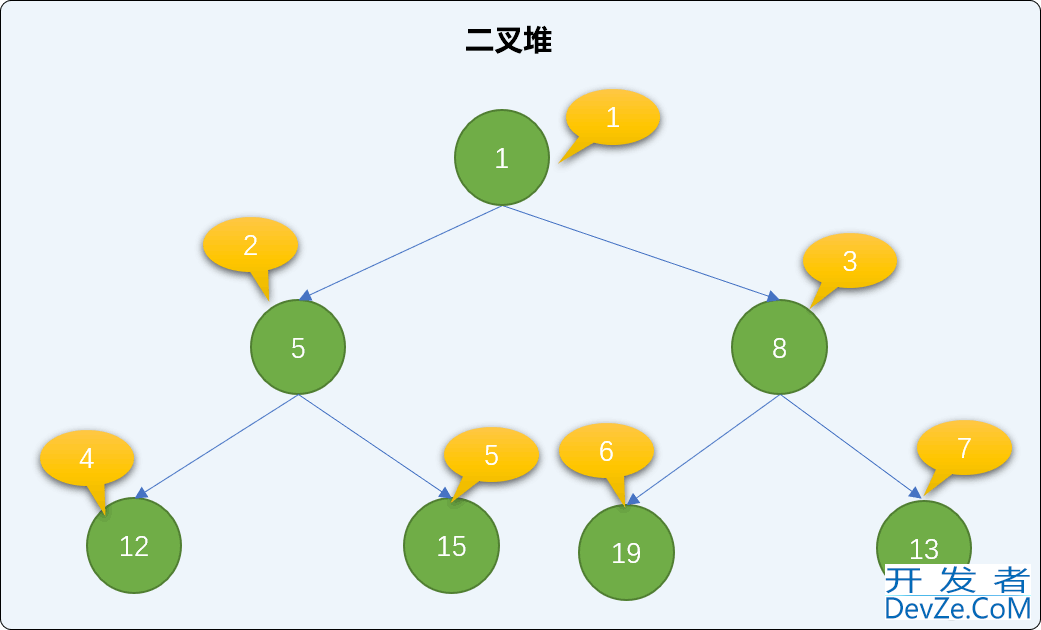
继续添加值为 15、19、8 的 3 个新结点，并检查二叉堆的状况。

int main(int argc, char** argv) {
	//省略……
	heap.insert(15);
	heap.insert(19);
	heap.insert(8);
	cout<<"测试三："<<endl;
	heap.findAll();
	return 0;
}

上沉算法同样可以使用递归实现。

/*
*递归实现插入
*/
template<typename T>
int Heap<T>::insert_(T  val) {
	//存储在最后一个位置
	int pos= ++Heap<T>::size;
	Heap<T>::heapList[pos]=val;
	//调用
	Heap<T>::insertByRecursion(pos);
}
template<typename T>
int Heap<T>::insertByRecursion(int  pos) {
//找到父结点位置
	int parentIdx=  pos / 2;
	if(parentIdx==0)
		//出口一，没有父结点
		return pos;
	if( Heap<T>::heapList[pos]>Heap<T>::heapList[parentIdx] )
		//出口二：大于父结点
		return pos;
	else {
		//和父亲结点交换
		int temp=Heap<T>::heapList[pos];
		Heap<T>::heapList[pos]=Heap<T>::heapList[parentIdx];
		Heap<T>::heapList[parentIdx]=temp;
		//递归 
		Heap<T>::insertByRecursion(parentIdx);
	}
}

2.4 下沉算法

介绍完添加方法后，再来了解一下，如何使用下沉算法删除二叉堆中的结点。

二叉堆的删除操作从根结点开始，如下图删除根结点后，空出来的根结点位置，需要在整个二叉堆中重新找一个结点充当新的根结点。

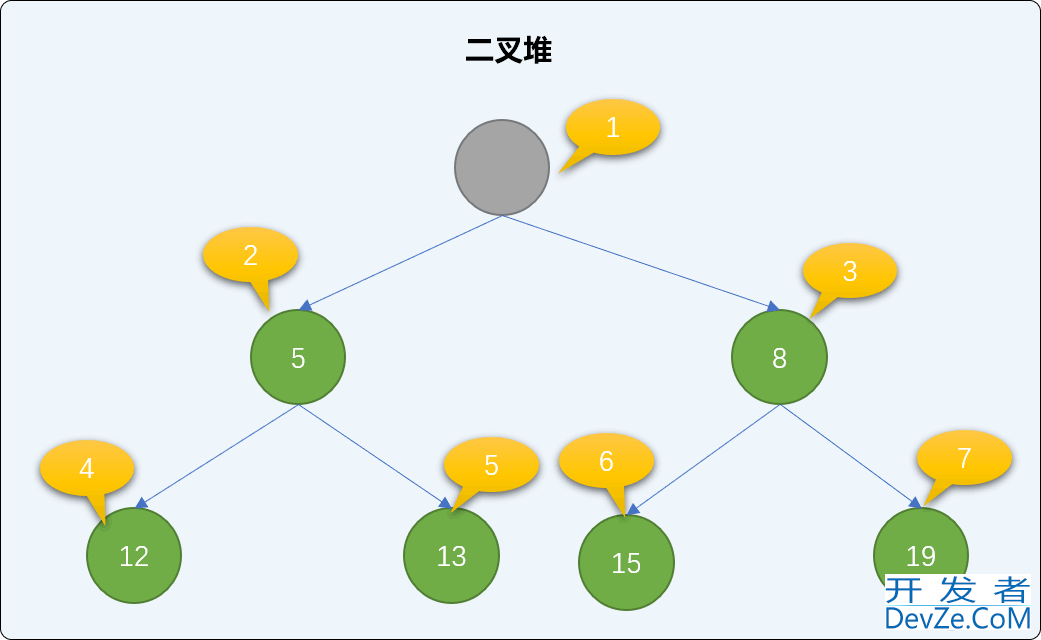
二叉堆中使用下沉算法选择新的根结点：

找到二叉堆中的最后一个结点，移到到根结点位置。如下图，把二叉堆中最后那个值为 19 的结点移到根结点位置。

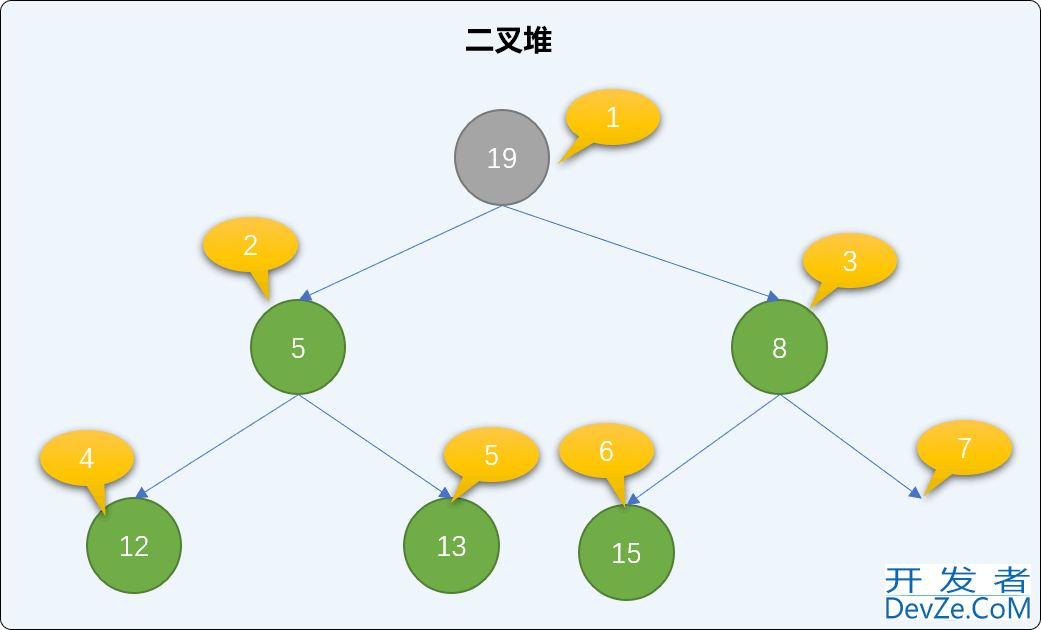
最小堆中，如果新的根结点的值比左或右子结点的值大，则和子结点交换位置。如下图，在二叉堆中把 19 和 5 的位置进行交换。

Tips： 总是和最小的子结点交换。

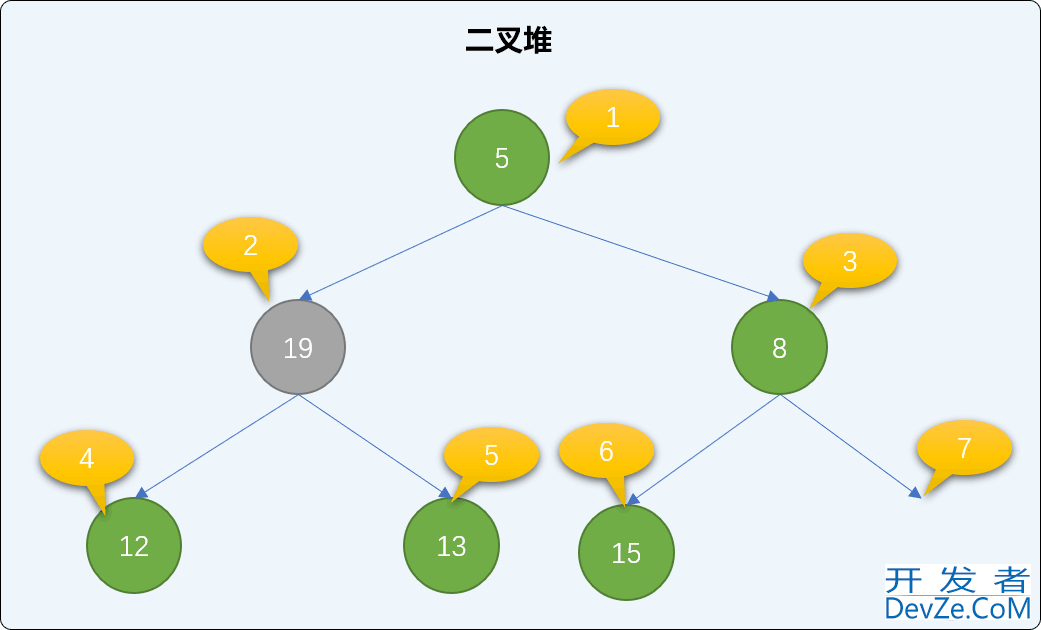
交换后，如果还是不满足最小二叉堆父结点小于子结点的规则，则继续比较、交换新根结点直到下沉到二叉堆有序为止。如下，继续交换 12 和 19 的值。如此反复经过多次交换直到整个堆结构符合二叉堆的特性。

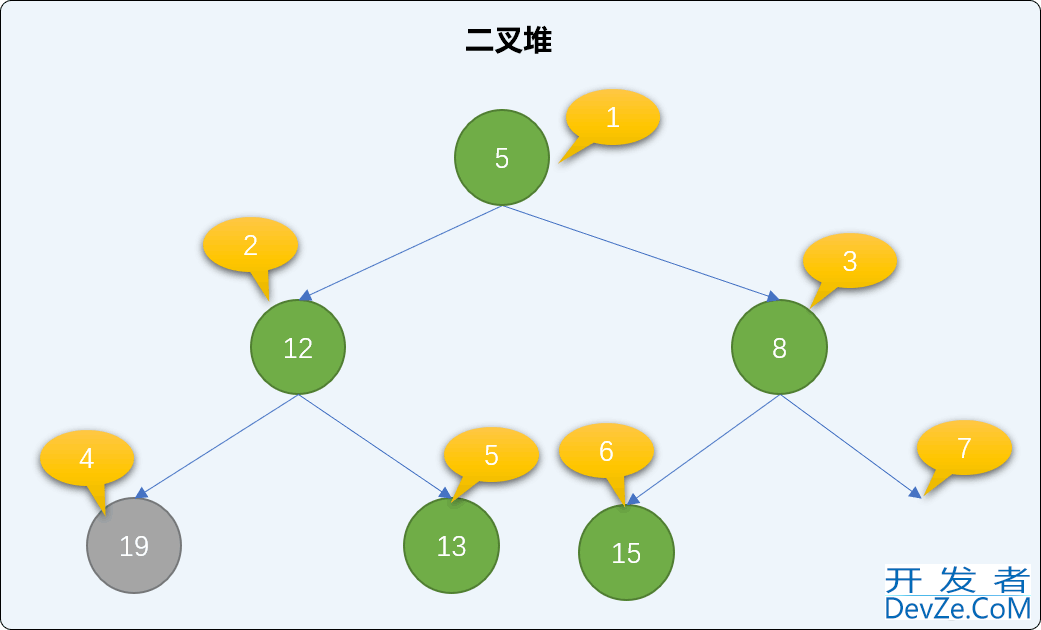
removeoot 方法的具体实现：

/*
* 下沉算法，删除结点
*/
template<typename T>
T Heap<T>::removeRoot() {
	if(Heap<T>::size==0)return NULL;
	T root=Heap<T>::heapList[1];
	if(Heap<T>::size==1) {
		Heap<T>::size--;
		return root;
	}
	//堆中最后一个结点移动根结点
	Heap<T>::heapList[1]=Heap<T>::heapList[Heap<T>::size];
	Heap<T>::size--;

	//下沉算法
	int parentIdx=1;
	//子结点值
	T minChild;
	//子结点位置
	int idx;
	while(1) {
		//左结点位置
		int leftIdx=parentIdx*2;
		//右结点位置
		int rightIdx=parentIdx*2+1;
		if( leftIdx<=Heap<T>::size && rightIdx<=Heap<T>::size ) {
			//记录较小的结点值和位置
			minChild=Heap<T>::heapList[leftIdx]<Heap<T>::heapList[rightIdx]?Heap<T>::heapList[leftIdx]:Heap<T>::heapList[rightIdx];
			idx=Heap<T>::heapList[leftIdx]<Heap<T>::heapList[rightIdx]?leftIdx:rightIdx;
		} else if( leftIdx<=Heap<T>::size) {
			minChild=Heap<T>::heapList[leftIdx];
			idx=leftIdx;
		} else if( rightIdx<=Heap<T>::size ) {
			minChild=Heap<T>::heapList[rightIdx];
			idx=rightIdx;
		}else{
			//没有子结点 
			break;
		}
		//是否交换
		if( Heap<T>::heapList[parentIdx]>minChild ) {
			Heap<T>::heapList[idx]=Heap<T>::heapList[parentIdx];
			Heap<T>::heapList[parentIdx]=minChild;
			parentIdx=idx;
		} else {
			break;
		}
	}
	return root;
} 

测试在二叉堆中删除结点：

int main(int argc, phpchar** argv) {
    //省略……
	cout<<"测试删除一:"<<endl;
	heap.removeRoot();
	heap.findAll();
	return 0;
}

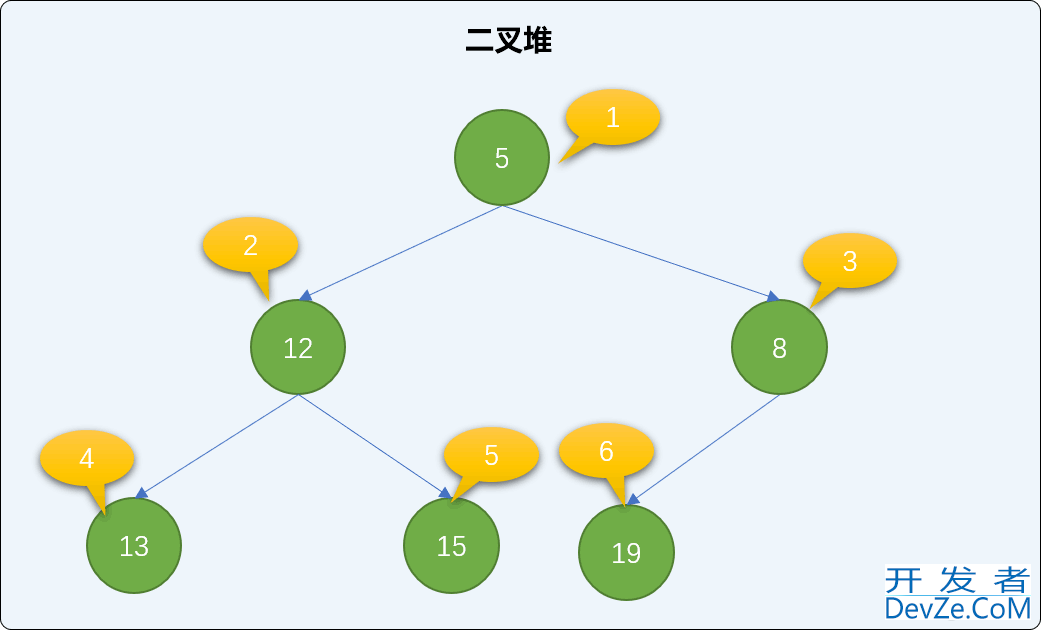
可以看到最后二叉堆的结构和有序性都得到了完整的保持。

"下沉算法" 同样可以使用递归实现。

/*
*递归实现下沉算法
*/
template<typename T>
T Heap<T>::removeRoot_() {
	if(Heap<T>::size==0)return NULL;
	//根结点值
	T root=Heap<T>::heapList[1];
	//
	if(Heap<T>::size==1) {
		Heap<T>::size--;
		return root;
	}
	//堆中最后一个结点移动根结点
	Heap<T>::heapList[1]=Heap<T>::heapList[Heap<T>::size];
	Heap<T>::size--;
	//调用
	Heap<T>::removeRootByRecursion(1);
	return root;
}

template<typename T>
void Heap<T>::removeRootByRecursion(int parentIdx ) {
	//子结点值
	T minChild;
	//子结点位置
	int idx;
	//左结点位置
	int leftIdx=parentIdx*2;
	//右结点位置
	int rightIdx=parentIdx*2+1;
	if( leftIdx<=Heap<T>::size && rightIdx<=Heap<T>::size ) {
		//记录较小的结点值和位置
		minChild=Heap<T>::heapList[leftIdx]<Heap<T>::heapList[rightIdx]?Heap<T>::heapList[leftIdx]:Heap<T>::heapList[rightIdx];
		idx=Heap<T>::heapList[leftIdx]<Heap<T>::heapList[rightIdx]?leftIdx:rightIdx;
	} else if( leftIdx<=Heap<T>::size) {
		minChild=Heap<T>::heapList[leftIdx];
		idx=leftIdx;
	} else if( rightIdx<=Heap<T>::size ) {
		minChild=Heap<T>::heapList[rightIdx];
		idx=rightIdx;
	} else {
		//没有子结点
		return;
	}
	//是否交换
	if( Heap<T>::heapList[parentIdx]>minChild ) {
		Heap<T>::heapList[idx]=Heap<T>::heapList[parentIdx];
		Heap<T>::heapList[parentIdx]=minChild;
        //递归
		Heap<T>::removeRootByRecursion(idx);
	} else {
		return;
	}
}

3. 堆排序

堆排序指借助堆的有序性对数据进行排序。

需要排序的数据以堆的方式保存。 然后再从堆中以根结点方式取出来，无序数据就会变成有序数据 。

如有数列=[4,1,8,12,5,10,7,21,3]，现通过堆的数据结构进行排序。

int main(int argc, char** argv) {
	//实例化堆
	Heap<int> heap;
	int nums[] = {4,1,8,12,5,10,7,21,3};
	int size=sizeof(nums)/4;
    // 创建根节点
	heap.setRoot(nums[0]);
    // 其它数据添加到二叉堆中
	for (int i=1; i<size; i++) {
		heap.insert(nums[i]);
	}
	cout<<"堆中数据："<<endl;
	heap.findAll();
    // 获取堆中的数据
	for(int i=0; i<size; i++ ) {
		nums[i]= heap.removeRoot();
		heap.findAll();
	}
	for(int i=0; i<size; i++)
		cout<<nums[i]<<"\t";
	return 0;
}

输出结果：

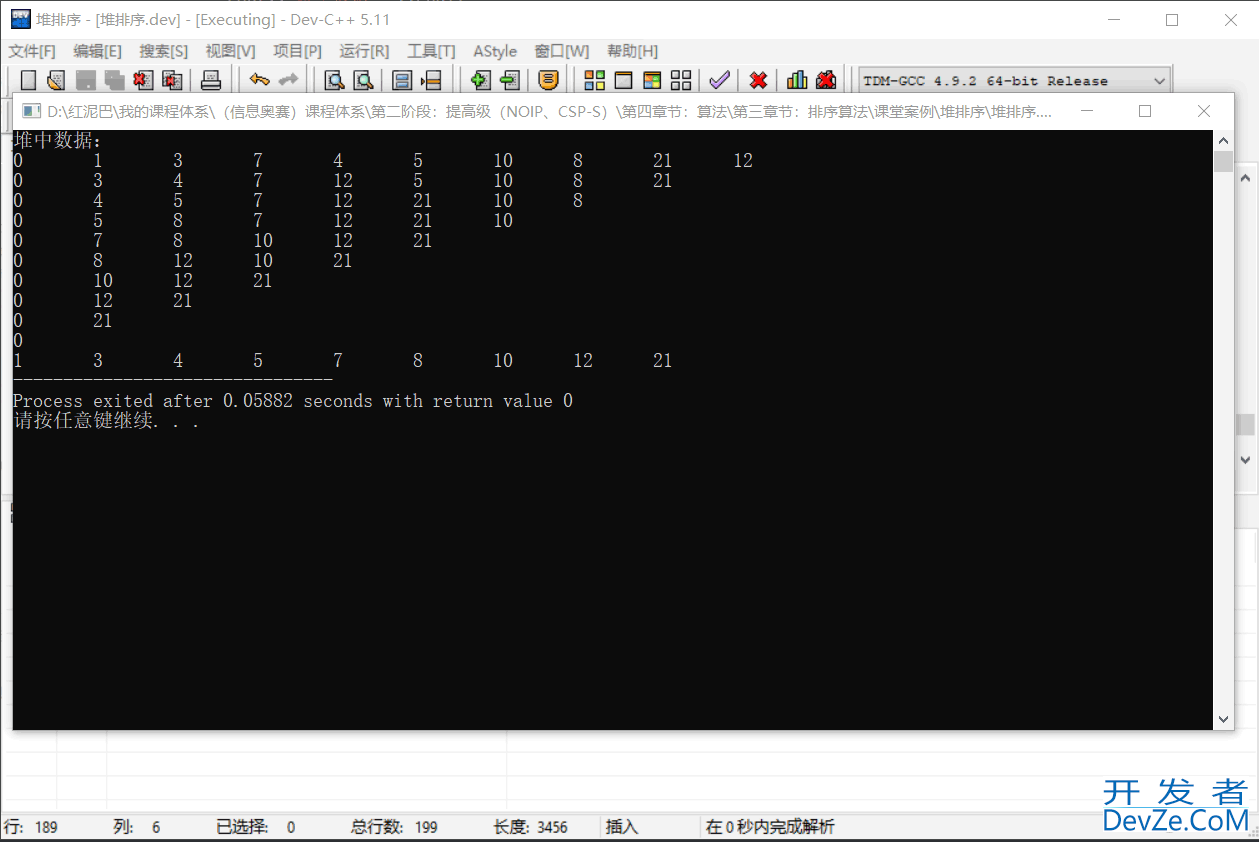
本例中的代码还有优化空间，本文试图讲清楚堆的使用，优化的地方交给有兴趣者。

4. 后记

在树结构上加上一些新特性要求，树会产生很多新的变种，如二叉树，限制子结点的个数，如满二叉树，限制叶结点的个数，如完全二叉树就是在满二叉树的“满”字上做点文章，让这个''满"变成"不那么满"。

在完全二叉树上添加有序性，则会衍生出二叉堆数据结构。利用二叉堆的有序性，能轻松完成对数据的排序。

到此这篇关于C++中二叉堆排序详解的文章就介绍到这了,更多相关C++ 二叉堆排序内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！