Python排序算法之堆排序算法

目录

• 1. 树
• 满二叉树的特性：
• 什么是完全二叉树？
• 完全二叉树的专业概念：
• 2. 二叉堆
• 2.1 二叉堆的抽象数据结构
• 2.2 API 实现
• 3. 堆排序
• 4. 后记

本文从树数据结构说到二叉堆数据结构，再使用二叉堆的有序性对无序数列排序。

1. 树

树是最基本的数据结构，可以用树映射现实世界中一对多的群体关系。如公司的组织结构、网页中标签之间的关系、操作系统中文件与目录结构……都可以用树结构描述。

树是由结点以及结点之间的关系所构成的集合。关于树结构的更多概念不是本文的主要内容，本文只关心树数据结构中的几个特殊变种：

二叉树

如果树中的任意结点（除叶子结点外）最多只有两个子结点，这样的树称为二叉树。

满二叉树

如果 二叉树中任意结点（除叶子结点外）都有 2 个子结点，则称为满二叉树。

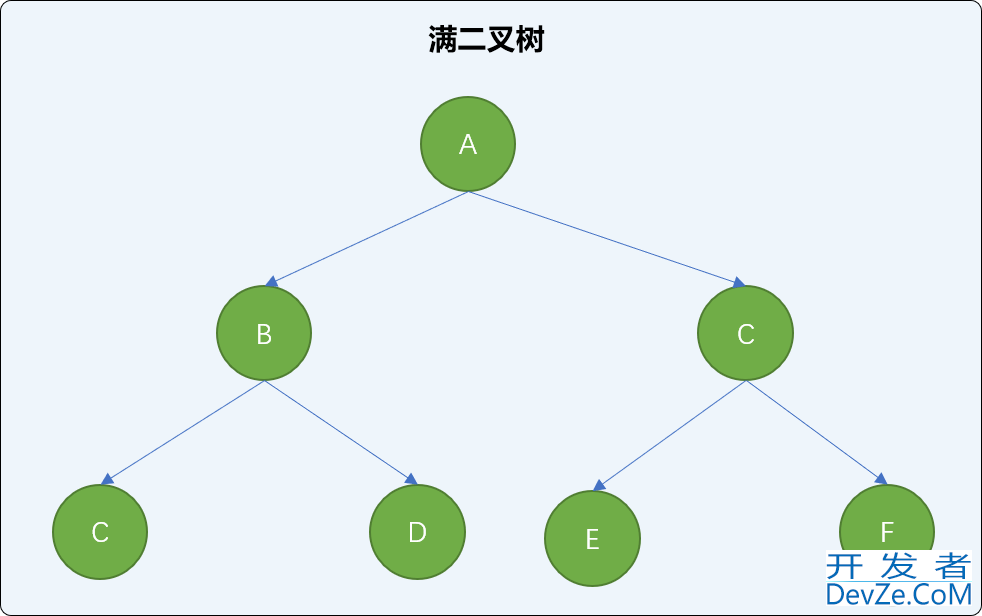
满二叉树的特性：

根据满二叉树的定义可知，满二叉树从上向下，每一层上的结点数以 2 倍的增量递增。也可以说，满二叉树是一个首项为 1 ，公比为 2 的等比数列。所以：

一个层数为 k 的满二叉树总结点数为：2^k-1 。

满二叉树的总结点数一定是奇数！

根据等比公式可知第 i 层上的结点数为：2^i-1，因此，一个层数为 k 的满二叉树的叶子结点个数为: 2^k-1。

什么是完全二叉树？

完全二叉树是满二叉树的一个特例。

通俗理解： 在满二叉树基础上，从右向左删除几个叶子节点后，此时满二叉树就变成了完全二叉树。如下图，在上图满二叉树基础上从右向左删除 2 个叶结点后的结构就是完全二叉树。

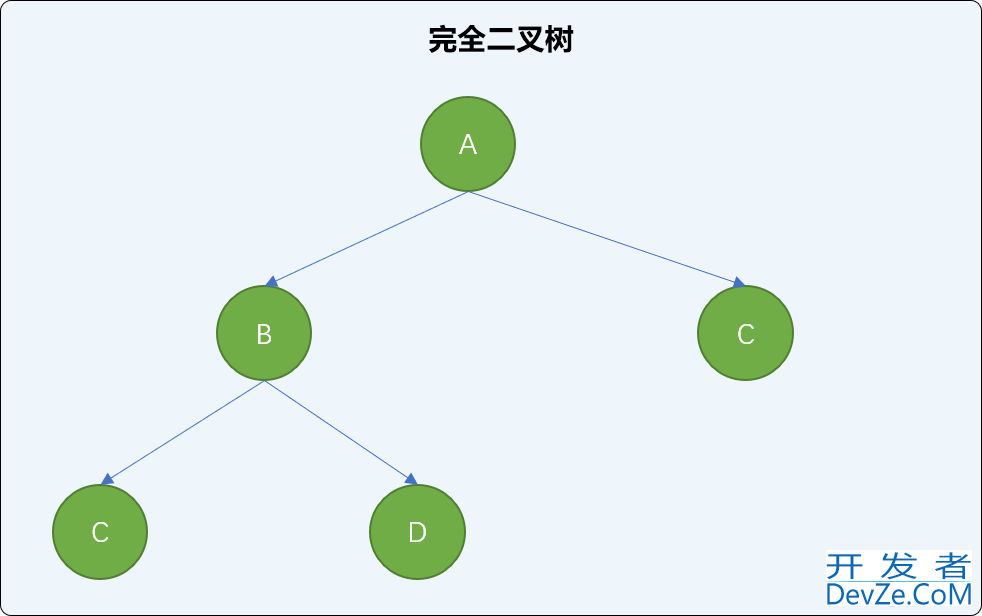
完全二叉树的专业概念：

一棵深度为 k 的有 n 个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为 i（1<=i<=n） 的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

专业概念有点像绕口令。

显然，完全二叉树的叶子结点只能出现在最下层或次下层，且最下层的叶子结点集中在树的左部。

注意：满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

2. 二叉堆

二叉堆是有序的 完全二叉树，在完全二叉树的基础上，二叉堆 提供了有序性特征：

二叉堆 的根结点上的值是整个堆中的最小值或最大值。

当根结点上的值是整个堆结构中的最小值时，此堆称为最小堆。

如果根结点上的值是整个堆结构中的最大值时，则称堆为最大堆。

最小堆中，任意节点的值大于父结点的值，反之，最大堆中，任意节点的值小于父结点的值。

综合所述，二叉堆的父结点与子结点之间满足下面的关系：

如果知道了一个结点的位置 i，则其左子结点在 2*i 处，右子结点在 2*i+1 处。

前提是结点要有子结点。

如果知道了一个结点的位置 i，则其父结点在 i除 2 处。

根结点没有父结点。

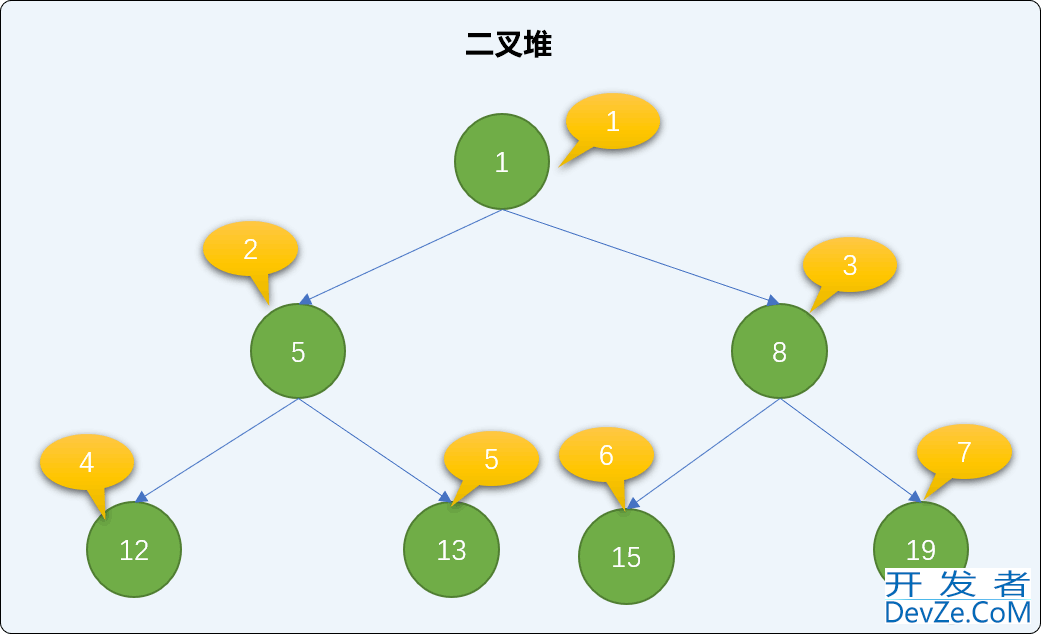
如上图所示：

值为 5 的结点在 2 处，则其左结点 12 的位置应该在 2*2=4 处，而实际情况也是在 4 位置。其右子结点 13 的位置应该在 2*2+1=5 的位置，实际位置也是在 5 位置。

值为 19 的结点现在 7 位置，其父结点的根据公式 7 除 2 等于 3(取整)，应该在 3 处，而实际情况也是在 3 处（位置在 3、 值为 8 的结点是其父结点）。

2.1 二叉堆的抽象数据结构

当谈论某种数据结构的抽象数据结构时，最基本的 API 无非就是增、删、改、查。

二叉堆的基本抽象数据结构：

Heap() ：创建一个新堆。 insert(data)： 向堆中添加新节点（数据）。 get_root()： 返回最小（大）堆的最小（大）元素。 remove_root() ：删除根节点。 is_empty()：判断堆是否为空。 find_all()：查询堆中所有数据。

二叉堆虽然是树结构的变种，有树的层次结构，但因结点与结点之间有很良好的数学关系，使用 python 中的列表存储是非常不错的选择。

现如有一个数列=[8,5编程,12,15,19,13,1]，现使用二叉堆方式保存。先构造一个列表。

列表中的第 0 位置初始为 0，从第 2 个位置也就是索引号为 1 的地方开始存储堆的数据。如下图，二叉堆中的数据在列表中的存储位置。

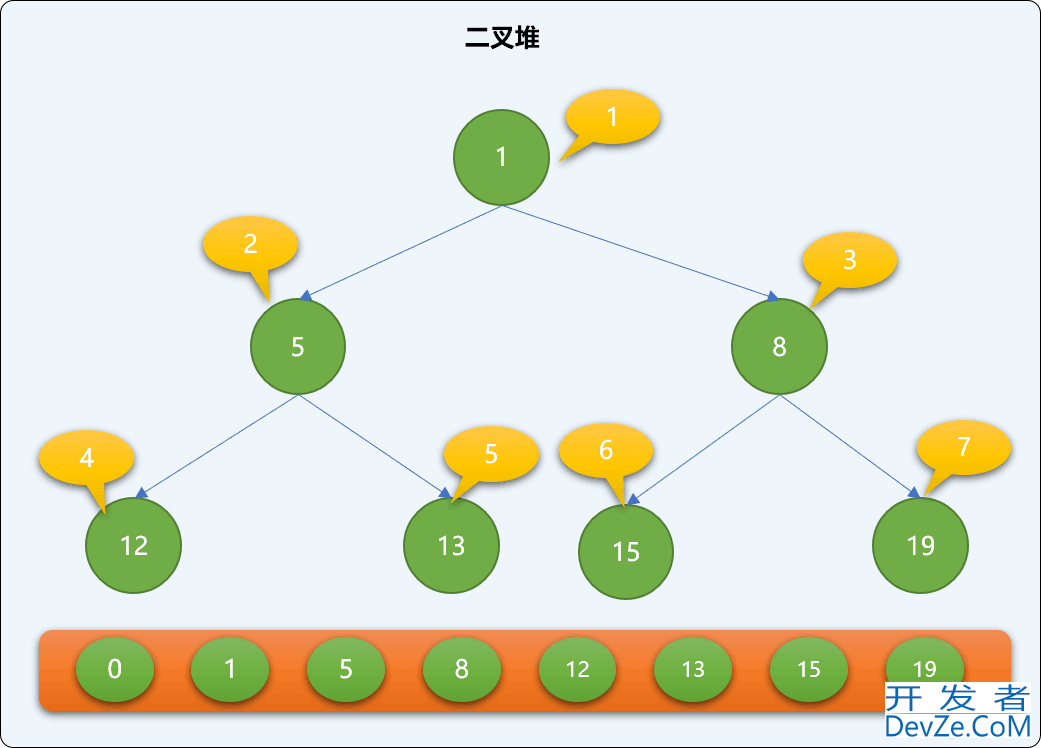
2.2 API 实现

设计一个 Heap 类封装对二叉堆的操作方法，类中方法用来实现最小堆。

'''
模拟最小堆
'''

class Heap():

    # 初始化方法
    def __init__(self):
        # 数列，第一个位置空着
        self.heap_list = [0]
        # 大小
        self.size = 0

    # 返回根结点的值
    def get_root(self):
		pass

    '''
    删除根结点
    '''
    def remove_root(self):
        pass

    # 为根结点赋值
    def set_root(self, data):
     	pass

    # 添加新结点
    def insert(self, data):
        pass

    # 是否为空
    def is_empty(self):
        pass

Heap 类中的属性详解：

heap_list：使用列表存储二叉堆的数据，初始时，列表的第 0 位置初始为默认值 0。

为什么要设置列表的第 0 位置的默认值为 0？

这个 0 也不是随意指定的，有其特殊数据含义：用来描述根结点的父结点或者说根结点没有父结点。

size：用来存储二叉堆中数据的实际个数。

Heap 类中的方法介绍：

is_empty：检查是不是空堆。

    # 长度为 0 ,则为空堆
    def is_empty(self):
        return self.size==0

set_root：创建根结点。保证根节点始终存储在列表索引为 1 的位置。

    # 为根结点赋值
    def set_root(self, data):
        self.heap_list.insert(1, data)
        self.size += 1

get_root：如果是最大堆，则返回二叉堆的最大值，如果是最小堆，则返回二叉堆的最小值。

    # 返回根结点的值
    def get_root(self):
        # 检查列表是否为空
        if not self.is_empty():
            return self.heap_list[1]
        raise Exception("空二叉堆！")

使用列表保存二叉堆数据时，根结点始终保存在索引号为 1 的位置。

前面是几个基本方法，现在实现添加新结点，编码之前，先要知道如何在二叉堆中添加新结点：

添加新结点采用上沉算法。如下演示流程描述了上沉的实现过程。

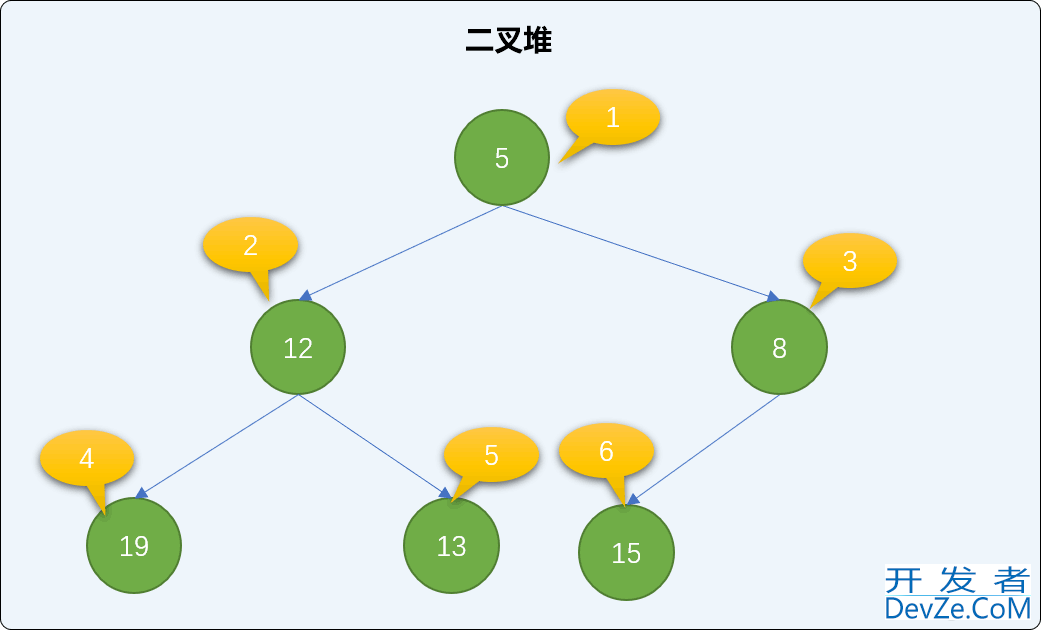
把新结点添加到已有的二叉堆的最后面。如下图，添加值为 4 的新结点，存储至索引号为 7 的位置。

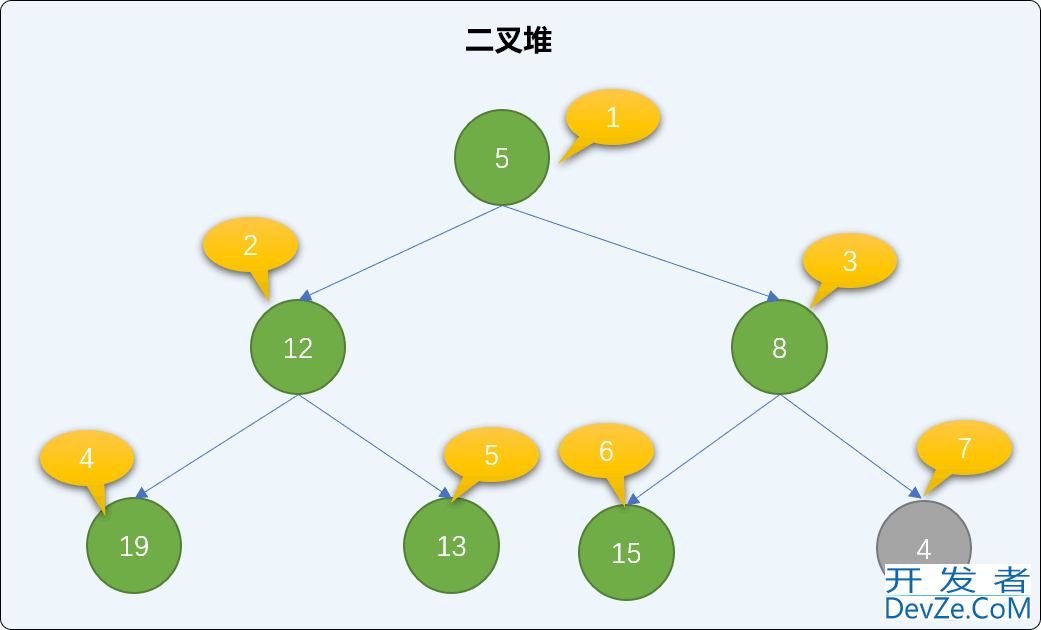
查找新结点的父结php点，并与父结点的值比较大小，如果比父结点的值小，则和父结点交换位置。如下图，值为 4 的结点小于值为 8 的父结点，两者交换位置。

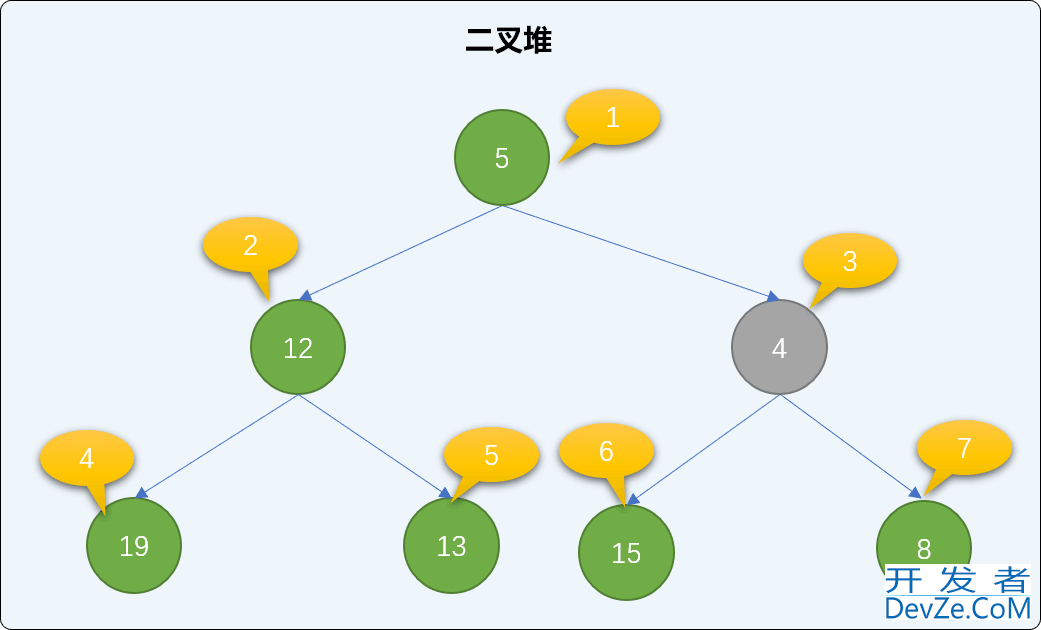
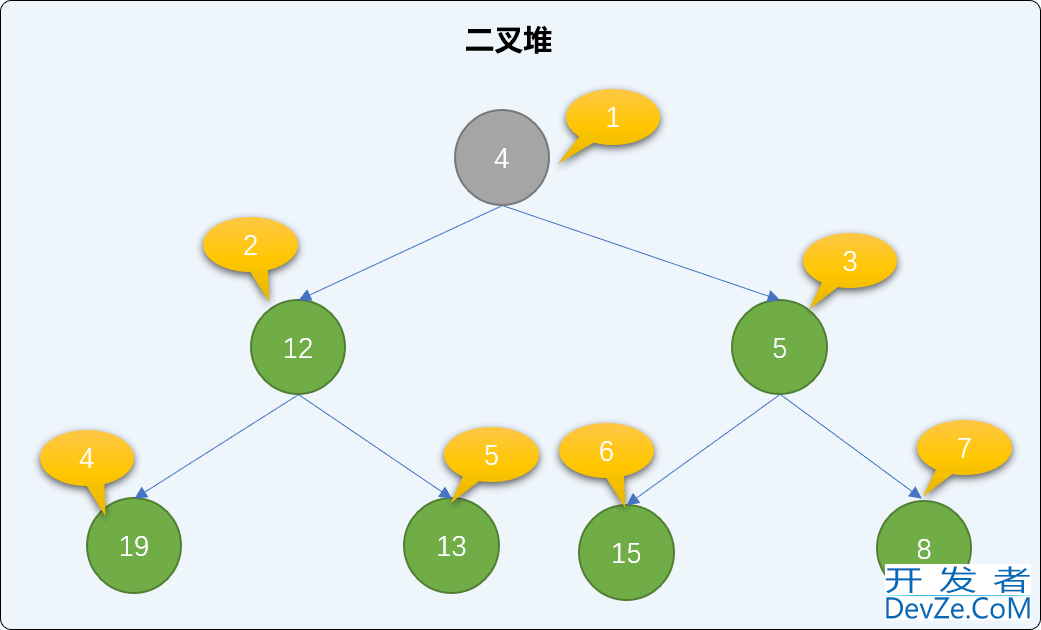
交换后再查询是否存在父结点，如果有，同样比较大小、交换，直到到达根结点或比父结点大为止。值为 4 的结点小于值为 5 的父结点，继续交换。交换后，新结点已经达到了根结点位置，整个添加过程可结束。观察后会发现，遵循此流程添加后，没有破坏二叉堆的有序性。

insert 方法的实现：

    # 添加新节点
 python   def insert(self, data):
        # 添加新节点至列表最后
        self.heap_list.append(data)
        self.size += 1
        # 新节点当前位置
        n_idx = len(self.heap_list) - 1
        while True:
            if n_idx // 2 == 0:
                # 当前节点是根节点，根结点编程客栈没有父结点，或说父结点为 0，这也是为什么初始化列表时设置 0 为默认值的原因
                break
            # 和父节点比较大小
            if self.heap_list[n_idx] < self.heap_list[n_idx // 2]:
                # 和父节点交换位置
                self.heap_list[n_idx], self.heap_list[n_idx // 2] = self.heap_list[n_idx // 2], self.heap_list[n_idx]
            else:
                # 出口之二
                break
            # 修改新节点的当前位置
            n_idx = n_idx // 2

测试向二叉堆中添加数据。

创建一个空堆。

heap = Heap()

创建值为 5 的根结点。

heap.set_root(5)

检查根结点是否创建成功。

val = heap.get_root()
print(val)
'''
输出结果
5
'''

添加值为 12和值为13 的 2 个新结点，检查添加新结点后整个二叉堆的有序性是否正确。

# 添加新结点
heap.insert(12)
heap.insert(13)
# 输入数列
print(heap.heap_list)
'''
输出结果
[0, 5, 12，13]
'''

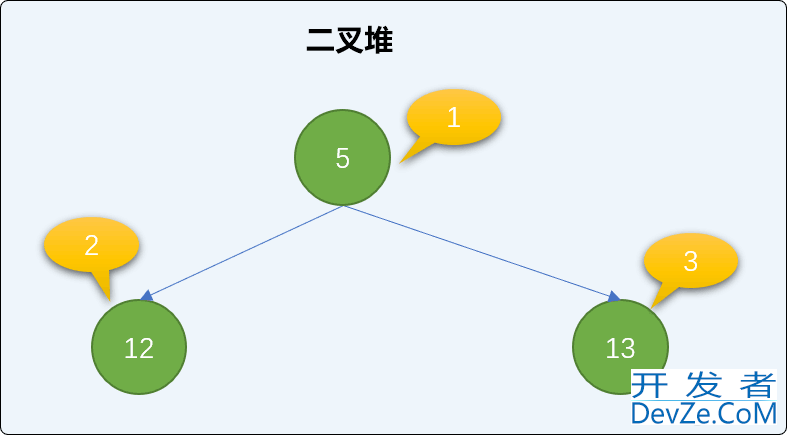
添加值为 1 的新结点，并检查二叉堆的有序性。

# 添加新结点
heap.insert(1)
print(heap.heap_list)
'''
输出结果
[0, 1, 5, 13, 12]
'''

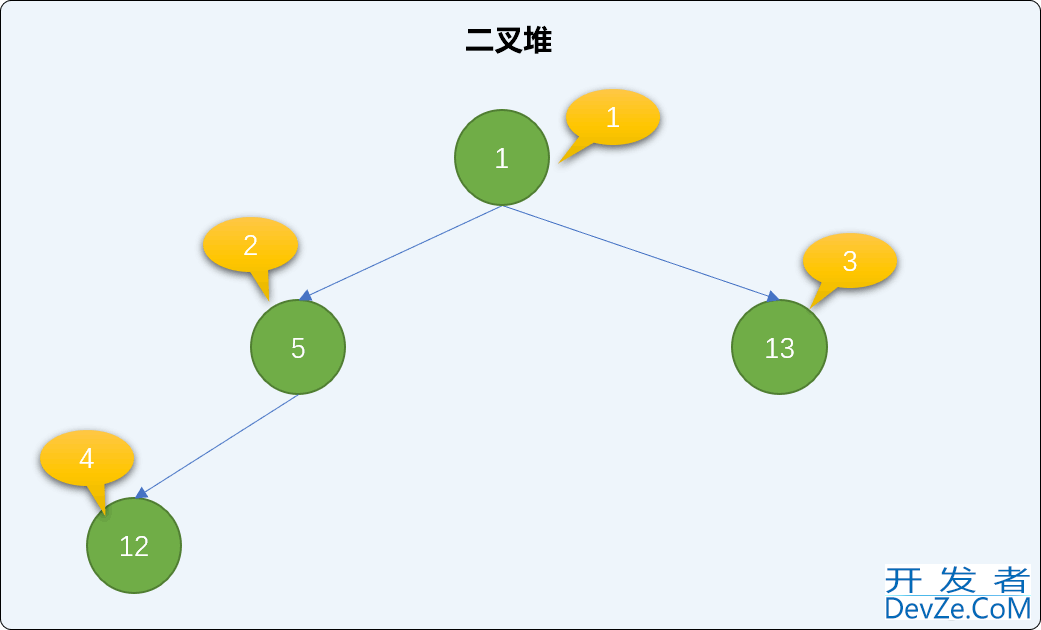
继续添加值为 15、19、8 的 3 个新结点，并检查二叉堆的状况。

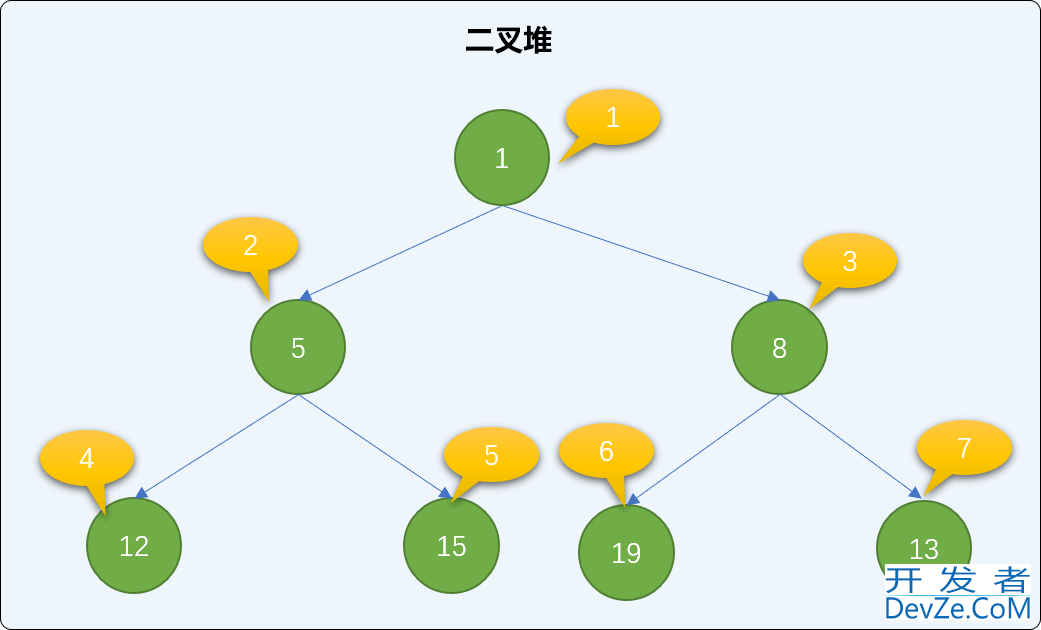
heap.insert(15)
heap.insert(19)
heap.insert(8)
print(heap.heap_list)
'''
输出结果
[0, 1, 5, 8, 12, 15, 19, 13]
'''

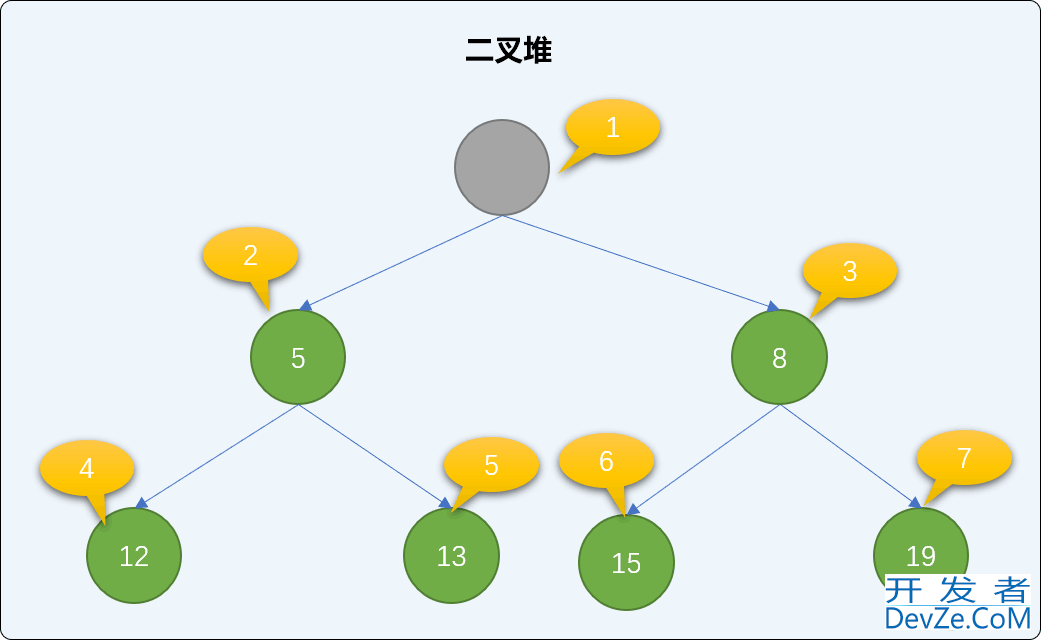
介绍完添加方法后，再来了解一下，如何删除二叉堆中的结点。

二叉堆的删除操作从根结点开始，如下图删除根结点后，空出来的根结点位置，需要在整个二叉堆中重新找一个结点充当新的根结点。

二叉堆中使用下沉算法选择新的根结点：

找到二叉堆中的最后一个结点，移到到根结点位置。如下图，把二叉堆中最后那个值为 19 的结点移到根结点位置。

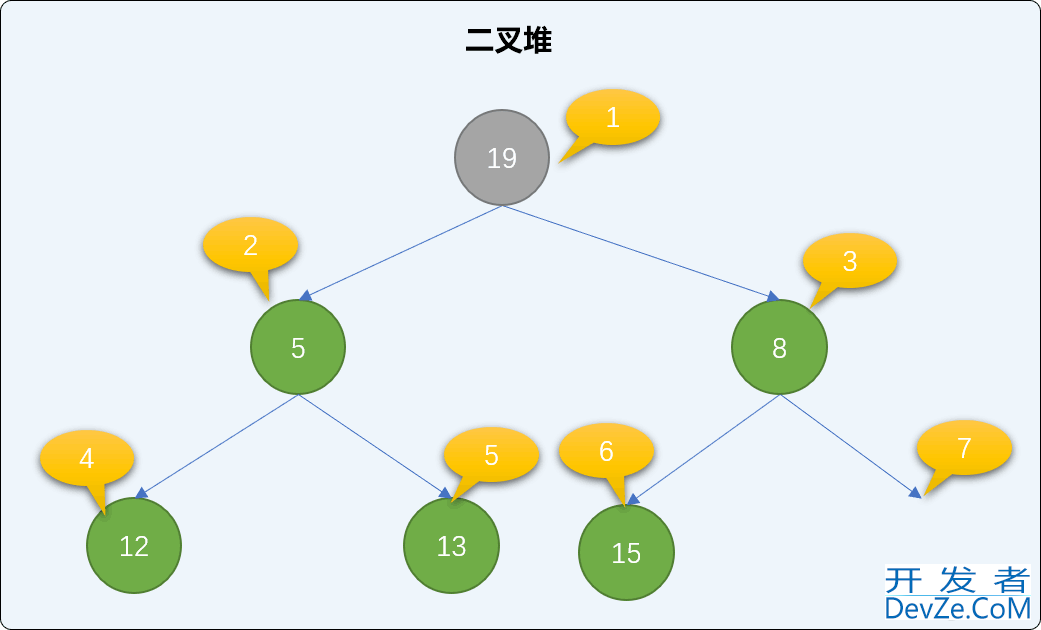
最小堆中，如果新的根结点的值比左或右子结点的值大，则和子结点交换位置。如下图，在二叉堆中把 19 和 5 的位置进行交换。

注意：总是和最小的子结点交换。

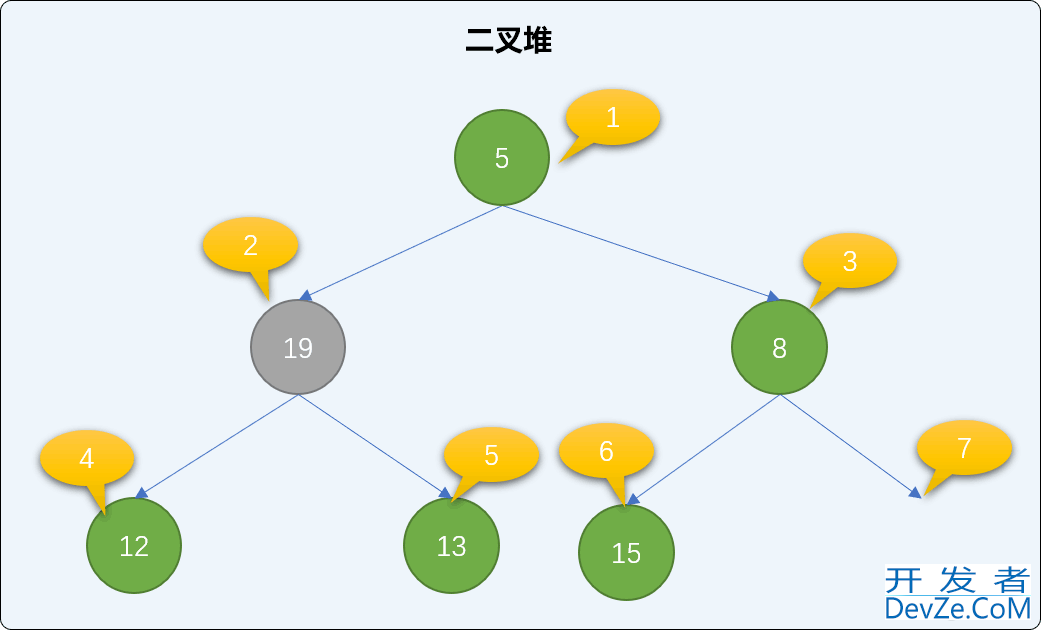
交换后，如果还是不满足最小二叉堆父结点小于子结点的规则，则继续比较、交换新根结点直到下沉到二叉堆有序为止。如下，继续交换 12 和 19 的值。如此反复经过多次交换直到整个堆结构符合二叉堆的特性。

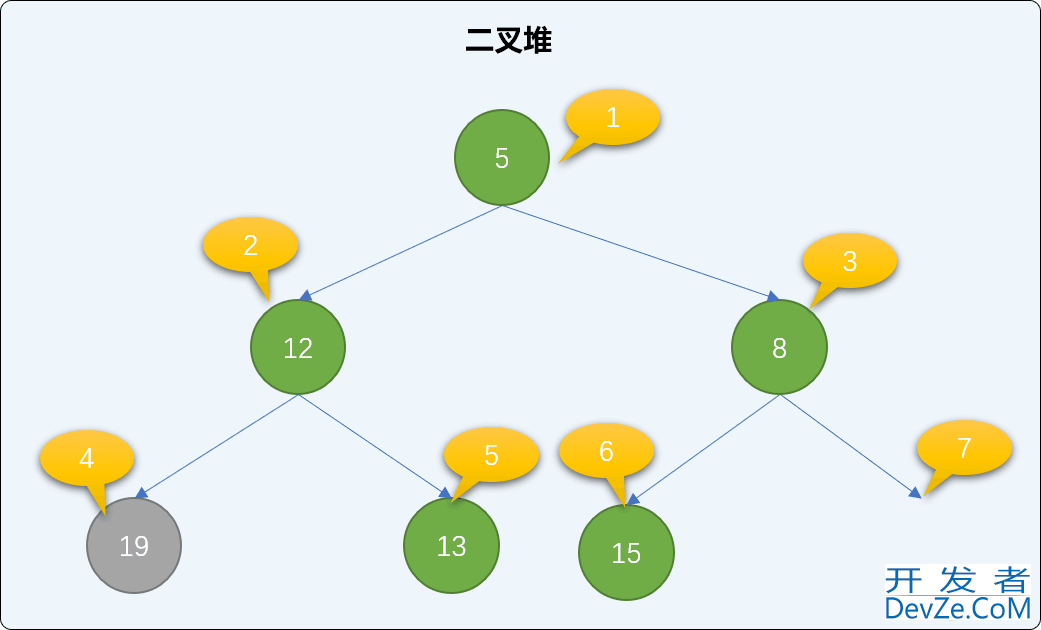
remove_root 方法的具体实现：

	'''
    删除根节点
    '''
    def remove_root(self):
        r_val = self.get_root()
        self.size -= 1
        if self.size == 1:
            # 如果只有根节点，直接删除
            return self.heap_list.pop()
        i = 1
        # 二叉堆的最后结点成为新的根结点
        self.heap_list[i] = self.heap_list.pop()
        # 查找是否存在比自己小的子结点
        while True:
            # 子结点的位置
            min_pos = self.min_child(i)
            if min_pos is None:
                # 出口：没有子结点或没有比自己小的结点
                break
            # 交换
            self.heap_list[i],HTPmnYP self.heap_list[min_pos] = self.heap_list[min_pos], self.heap_list[i]
            i = min_pos
        return r_val

    '''
    查找是否存在比自己小的子节点
    '''
    def min_child(self, i):
        # 是否有子节点
        child_pos = self.is_exist_child(i)
        if child_pos is None:
            # 没有子结点
            return None
        if len(child_pos) == 1 and self.heap_list[i] > self.heap_list[child_pos[0]]:
            # 有 1 个子节点，且大于此子结点
            return child_pos[0]
        elif len(child_pos) == 2:
            # 有 2 个子节点，找到 2 个结点中小的那个结点
            if self.heap_list[child_pos[0]] < self.heap_list[child_pos[1]]:
                if self.heap_list[i] > self.heap_list[child_pos[0]]:
                    return child_pos[0]
            else:
                if self.heap_list[i] > self.heap_list[child_pos[1]]:
                    return child_pos[1]

    '''
    检查是否存在子节点
    返回具体位置
    '''
    def is_exist_child(self, p_idx):
        # 左子节点位置
        l_idx = p_idx * 2
        # 右子节点位置
        r_idx = p_idx * 2 + 1
        if l_idx <= self.size and r_idx <= self.size:
            # 存在左、右子节点
            return l_idx, r_idx
        elif l_idx <= self.size:
            # 存在左子节点
            return l_idx,
        elif r_idx <= self.size:
            # 存在右子节点
        return r_idx,

remove_root 方法依赖 min_child和is_exist_child 方法：

min_child 方法用查找比父结点小的结点。

is_exist_child 方法用来查找是否存在子结点。

测试在二叉堆中删除结点：

heap = Heap()
heap.set_root(5)
val = heap.get_root()
print(val)

# 添加新结点
heap.insert(12)
heap.insert(13)
# 添加新结点
heap.insert(1)
heap.insert(15)
heap.insert(19)
heap.insert(8)
# 添加结点后二叉堆现状
print("添加结点后二叉堆现状：", heap.heap_list)
val = heap.remove_root()
print("删除根结点后二叉堆现状：", heap.heap_list)
'''
输出结果
添加节点后二叉堆现状： [0, 1, 5, 8, 12, 15, 19, 13]
删除根节点后二叉堆现状： [0, 5, 12, 8, 13, 15, 19]
'''

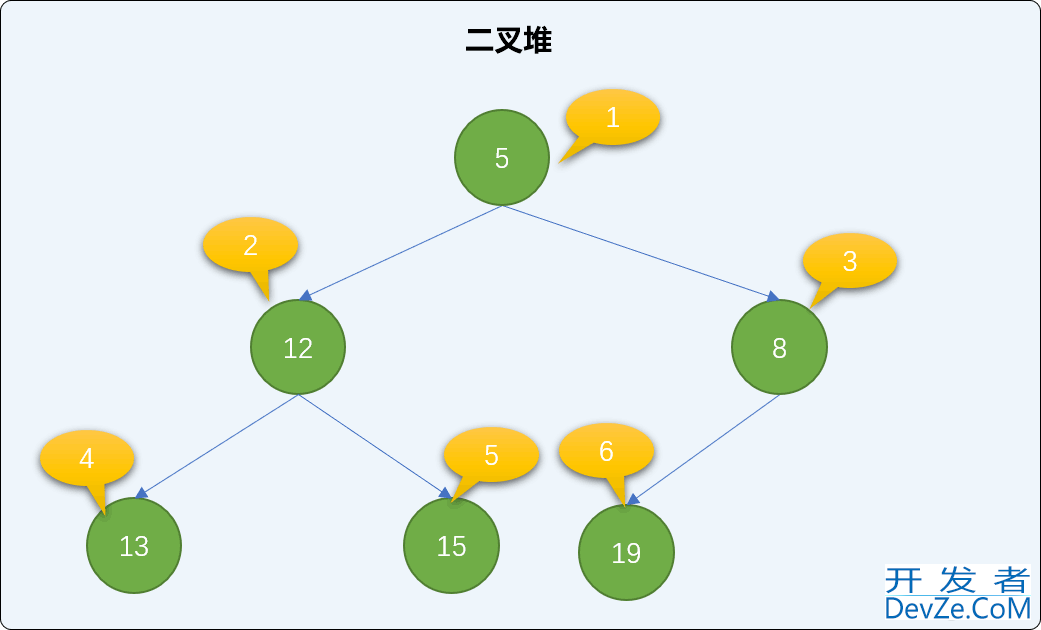
可以看到最后二叉堆的结构和有序性都得到了完整的保持。

3. 堆排序

堆排序指借助堆的有序性对数据进行排序。

需要排序的数据以堆的方式保存 然后再从堆中以根结点方式取出来，无序数据就会变成有序数据 。

如有数列=[4,1,8,12,5,10,7,21,3]，现通过堆的数据结构进行排序。

heap = Heap()
nums = [4,1,8,12,5,10,7,21,3]
# 创建根节点
heap.set_root(nums[0])
# 其它数据添加到二叉堆中
for i in range(1, len(nums)):
    heap.insert(nums[i])
print("堆中数开发者_开发培训据：", heap.heap_list)
# 获取堆中的数据
nums.clear()
while heap.size > 0:
    nums.append(heap.remove_root())
print("排序后数据：", nums)
'''
输出结果
堆中数据： [0, 1, 3, 7, 4, 5, 10, 8, 21, 12]
排序后数据： [1, 3, 4, 5, 7, 8, 10, 12, 21]
'''

本例中的代码还有优化空间，本文试图讲清楚堆的使用，优化的地方交给有兴趣者。

4. 后记

在树结构上加上一些新特性要求，树会产生很多新的变种，如二叉树，限制子结点的个数，如满二叉树，限制叶结点的个数，如完全二叉树就是在满二叉树的“满”字上做点文章，让这个''满"变成"不那么满"。

在完全二叉树上添加有序性，则会衍生出二叉堆数据结构。利用二叉堆的有序性，能轻松完成对数据的排序。

二叉堆中有 2 个核心方法，插入和删除，这两个方法也可以使用递归方式编写。

以上就是Python排序算法之堆排序算法的详细内容，更多关于Python 堆排序算法的资料请关注我们其它相关文章！