Python动态演示旋转矩阵的作用详解

目录

• 先新建一组散点充当坐标轴
• 旋转矩阵与初步演示
• 转动次序对旋转的影响
• 动态演示旋转过程
• 总结

先新建一组散点充当坐标轴

为了比较直观地展示旋转过程，这里通过散点来新建三个坐标轴，通过对这三个坐标轴的转动，来直观地展现转动矩阵对坐标变换的影响。

import numpy as np
import matplotlib.pyplot as plt

def setAxis(N, axis=0):
    xs = np.arange(N)
    ys = np.zeros_like(xs)
    zs =js np.zeros_like(xs)
    if axis==0 : return [xs, ys, zs]
    elif axis==1 : return [ys, xs, zs]
    else编程: return [ys, zs, xs]

def drawAxis(X,Y,Z):
    ax = plt.subplot(projection='3d')
    ax.scatter(*X, c='r')
    ax.scatter(*Y, c='g')
    ax.scatter(*Z, c='b')
    plt.show()

X = setAxis(10, 0)
Y = setAxis(10, 1)
Z = setAxis(10, 2)    
drawAxis(X, Y, Z)

效果为

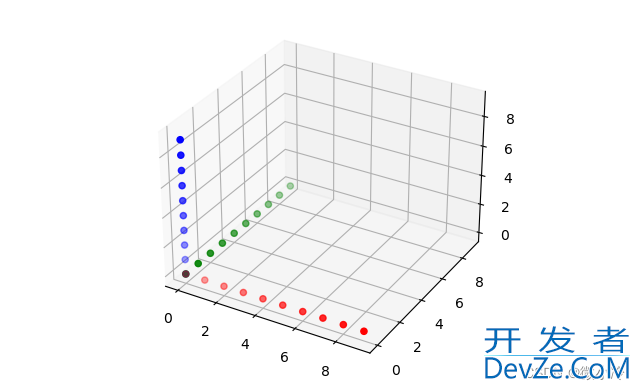
旋转矩阵与初步演示

欧拉角是用来唯一地确定定点转动刚体位置的三个一组独立角参量，由章动角θ、进动角ψ和自转角φ组成，为L.欧拉首先提出，故得名。

为了尽快进入演示部分，故对原理的介绍从略，仅从二维平面上的旋转矩阵出发，做一个简单的推导，而三维旋转矩阵，至少在形式上与二维是雷同的。

假设坐标系中有一个向量 ( x , y )，其模长为

，角度为

。若将其围绕坐标原点逆python时针旋转 θ \theta θ，则其坐标变为

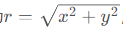
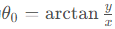
由于

，则上式可以写为

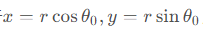
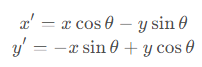
写成矩阵形式即为

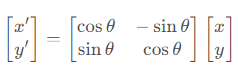
也就是说，在平面直角坐标系上，向量绕原点顺时针旋转 θ \theta θ，相当于左乘一个旋转矩阵。

推广到三维，为了限制 x y xy xy坐标平面上的旋转，要将其旋转中心从原点扩展为绕着 z z z轴旋转，从而三维旋转矩阵可推广为

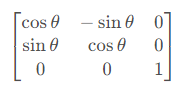
同理可得到绕三个轴转动的旋转矩阵，为了书写方便，记

，可列出下表。

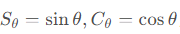
下面用lambda表达式来实现，用以描述单个轴的旋转过程。

import numpy as np
# 将角度转弧度后再求余弦
cos = lambda th : np.cos(np.deg2rad(th))
sin = lambda th : np.sin(np.deg2rad(th))

# 即 Rx(th) => Matrix
Rx = lambda th : np.array([
    [1, 0,       0],
    [0, cos(th), -sin(th)],
    [0, sin(th), cos(th)]])
Ry = lambda th : np.array([
    [cos(th),  0, sin(th)],
    [0      ,  1, 0],
    [-sin(th), 0, cos(th)]
])
Rz = lambda th : np.array([
    [cos(th) , sin(th), 0],
    [-sin(th), cos(th), 0],
    [0       , 0,       1]])

有了旋转矩阵，就可以旋转，接下来让坐标轴沿着三个轴分别旋转30°，其效果如下

代码如下

def drawAxis(X, Y, Z, fig, i):
    ax = fig.add_subplot(1,3,i,projection='3d')
    ax.plot(*X, c='r')
    ax.plot(*Y, c='g')
    ax.plot(*Z, c='b')

Xx, Yx, Zx = Rx(30) @ X, Rx(30) @ Y, Rx(30) @ Z
Xy, Yy, Zy = Ry(30) @ X, Ry(30) @ Y, Ry(30) @ Z
Xz, Yz, Zz = Rz(30) @ X, Rz(30) @ Y, Rz(30) @ Z

fig = plt.figure("rotate")
drawAxis(Xx, Yx, Zx, fig, 1)
drawAxis(Xy, Yy, Zy, fig, 2)
drawAxis(Xz, Yz, Zz, fig, 3)

plt.show()

转动次序对旋转的影响

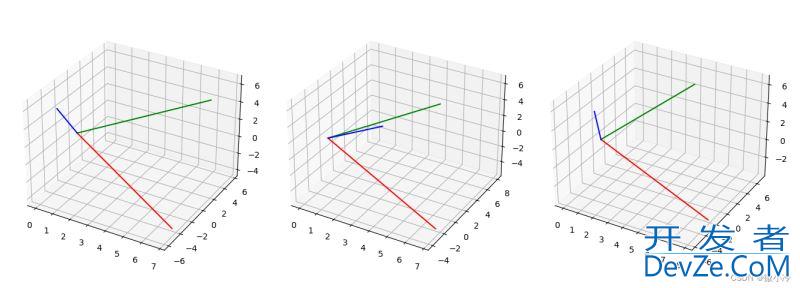
由于旋转被建开发者_Go开发模成了矩阵，而众所周知矩阵乘法是不可交换的，也就是说，就算绕着三个坐标轴旋转相同的角度，也会因为转动次序不同而引发不同的结果。

XYZ = [X, Y, Z]
R_xyz = [Rz(30) @ Ry(30) @ Rx(30) @ R for R in XYZ]
R_zyx = [Rx(30) @ Ry(30) @ Rz(30) @ R for R in XYZ]
R_yxz = [Rz(30) @ Rx(30) @ Ry(30) @ R for R in XYZ]

fig = plt.figure("rotate")
drawAxis(*R_xyz, fig, 1)
drawAxis(*R_zyx, phpfig, 2)
drawAxis(*R_yxz, fig, 3)

plt.show()

得到下图

动态演示旋转过程

30°的转动之后，坐标轴变得面目全非，接下来要做的就是动态绘制这三个坐标轴的旋转过程

from numpy.random import rand
from matplotlib import animation

Rot = [Rx, Ry, Rz]
# 根据指定坐标轴顺序来以指定角度旋转向量
def rotVec(vec, axis, degs):
    for i in range(len(axis)):
        vec = Rot[axis[i]](degs[i]) @ vec
    return vec

# 若x在[a,b]区间，则对a取模，若小于a置0，大于b为b-a
def truncMod(x, a, b):
    if x < a : return 0
    elif x >= b : return b-a
    else : return x%(b-a)

# 三个坐标轴
XYZ = [setAxis(10,i) for i in isRmsWWcrange(3)]

fig = plt.figure(figsize=(5,5))
ax = fig.add_subplot(projection='3d')
ax.grid()

lines = [ax.plot([],[],[], '-', lw=0.5, c=c)[0] 
    for c in 'rgb']

def animate(n):
    # 按照xyz顺序旋转
    axis = [2,1,0]
    degs = [truncMod(n, st, st + 30) for st in [0,30,60]]
    newXYZ = [rotVec(x, axis, degs) for x in XYZ]
    for i in range(3):
        lines[i].set_data(newXYZ[i][0],newXYZ[i][1])
        lines[i].set_3d_properties(newXYZ[i][2])
    return lines

ani = animation.FuncAnimation(fig, animate, 
    range(90), interval=50, blit=True)

#plt.show()
ani.save("zyx.gif")

效果如下

x-y-z

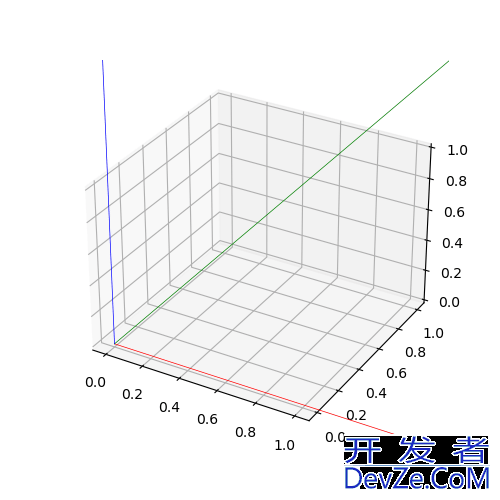
z-y-x

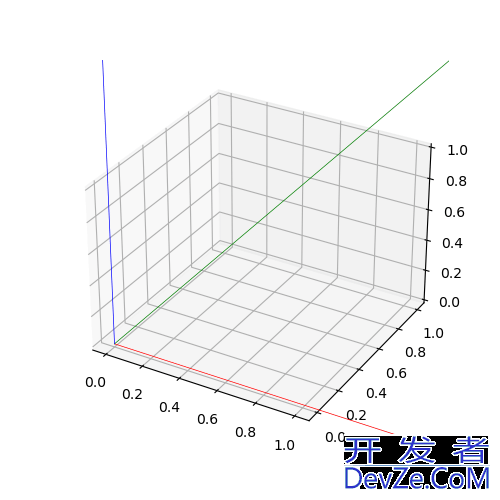
总结

到此这篇关于python动态演示旋转矩阵作用的文章就介绍到这了,更多相关Python动态演示旋转矩阵内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！