目录
- 一:手写数字模型构建与保存
- 1 加载数据集
- 2 特征数据 标签数据
- 3 训练集 测试集
- 4 数据流图 输入层
- 5 隐藏层
- 6 损失函数
- 7 梯度下降算法
- 8 输出损失值
- 9 模型 保存与使用
- 10 完整源码分享
- 二:手写数字模型使用与测试
一:手写数字模型构建与保存
1 加载数据集
# 1加载数据 digits_data = load_digits()
可以先简单查看下 手写数字集,如下可以隐约看出数字为8
pltwww.devze.com.imshow(digits_data.images[8]) plt.show()
2 特征数据 标签数据
# 数据划分 x_data = digits_data.data y_data = digits_data.target
3 训练集 测试集
# 训练集 + 测试集 x_test = x_data[:40] y_test = y_data[:40] x_train = x_data[40:] y_train = y_data[40:] # 概率问题 y_train_2 = np.zeros(shape=(len(y_train), 10))
4 数据流图 输入层
input_size = digits_data.data.shape[1] # 输入的列数 # 数据流图的构建 # x:输入64个特征值--像素 x = tf.placeholder(np.float32, shape=[None, input_size]) # y:识别的数字 有几个类别[0-9] y = tf.placeholder(np.float32, shape=[None, 10])
5 隐藏层
5.1 第一层
# 第一层隐藏层 # 参数1 输入维度 参数2:输出维度(神经http://www.devze.com元个数) 标准差是0.1的正态分布 w1 = tf.Variable(tf.random_normal([input_size, 80], stddev=0.1)) # b的个数就是隐藏层神经元的个数 b1 = tf.Variable(tf.constant(0.01), [80]) # 第一层计算 one = tf.matmul(x, w1) + b1 # 激活函数 和0比 大于0则激活 op1 = tf.nn.relu(one)
5.2 第二层
# 第二层隐藏层 上一层输出为下一层输入 # 参数1 输入维度 参数2:输出维度(神经元个数) 标准差是0.1的正态分布 w2 = tf.Variable(tf.random_normal([80, 10], stddev=0开发者_JAVA入门.1)) # b的个数就是隐藏层神经元的个数 b2 = tf.Variable(tf.constant(0.01), [10]) # 第一层计算 two = tf.matmul(op1, w2) + b2 # 激活函数 和0比 大于0则激活 op2 = tf.nn.relu(two)
6 损失函数
# 构建损失函数 loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=op2))
7 梯度下降算法
# 梯度下降算法 Optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.005).minimize(loss)
8 输出损失值
# 变量初始化
init = tf.global_variables_initializer()
data_size = digits_data.data.shape[0]
# 开启会话
with tf.Session() as sess:
sess.run(init)
# 训练次数
for i in range(500):
编程客栈 # 数据分组
start = (i * 100) % data_size
end = min(start + 100, data_size)
BATch_x = x_train[start:end]
batch_y = y_train_2[start:end]
sess.run(Optimizer, feed_dict={x: batch_x, y: batch_y})
# 输出损失值
train_loss = sess.run(loss, feed_dict={x: batch_x, y: batch_y})
print(train_loss)
9 模型 保存与使用
obj = tf.train.Saver()
# 模型保存
obj.save(sess, 'model-digits.ckpt')
10 完整源码分享
import tensorflow as tf
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# 1加载数据
digits_data = load_digits()
# 查看数据
# print(digits_data)
# 查看数据基本特征 (1797, 64) 64:8*8像素点
# print(digits_data.data.shape)
# plt.imshow(digits_data.images[8])
# plt.show()
# 数据划分
x_data = digits_data.data
y_data = digits_data.target
# 训练集 + 测试集
x_test = x_data[:40]
y_test = y_data[:40]
x_train = x_data[40:]
y_train = y_data[40:]
# 概率问题
y_train_2 = np.zeros(shape=(len(y_train), 10))
# 对应的分类 当前行对应列变成1
for index, row in enumerate(y_train_2):
# 当前行 对应的数字对应列
row[int(y_train[index])] = 1
# print(y_train_2[0])
input_size = digits_data.data.shape[1] # 输入的列数
# 数据流图的构建
# x:输入64个特征值--像素
x = tf.placeholder(np.float32, shape=[None, input_size])
# y:识别的数字 有几个类别[0-9]
y = tf.placeholder(np.float32, shape=[None, 10])
# 第一层隐藏层
# 参数1 输入维度 参数2:输出维度(神经元个数) 标准差是0.1的正态分布
w1 = tf.Variable(tf.random_normal([input_size, 80], stddev=0.1))
# b的个数就是隐藏层神经元的个数
b1 = tf.Variable(tf.constant(0.01), [80])
# 第一层计算
one = tf.matmul(x, w1) + b1
# 激活函数 和0比 大于0则激活
op1 = tf.nn.relu(one)
# 第二层隐藏层 上一层输出为下一层输入
# 参数1 输入维度 参数2:输出维度(神经元个数) 标准差是0.1的正态分布
w2 = tf.Variable(tf.random_normal([80, 10], stddev=0.1))
# b的个数就是隐藏层神经元的个数
b2 = tf.Variable(tf.constant(0.01), [10])
# 第一层计算
two = tf.matmul(op1, w2) + b2
# 激活函数 和0比 大于0则激活
op2 = tf.nn.relu(two)
# 构建损失函数
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=op2))
# 梯度下降算法 优化器 learning_rate学习率(步长)
Optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.005).minimize(loss)
# 变量初始化
init = tf.global_variables_initializer()
data_size = digits_data.data.shape[0]
# 开启会话
with tf.Session() as sess:
sess.run(init)
# 训练次数
for i in range(500):
# 数据分组
start = (i * 100) % data_size
end = min(start + 100, data_size)
batch_x = x_train[start:epythonnd]
batch_y = y_train_2[start:end]
sess.run(Optimizer, feed_dict={x: batch_x, y: batch_y})
# 输出损失值
train_loss = sess.run(loss, feed_dict={x: batch_x, y: batch_y})
print(train_loss)
obj = tf.train.Saver()
# 模型保存
obj.save(sess, 'modelSave/model-digits.ckpt')
损失值在0.303左右,如下图所示
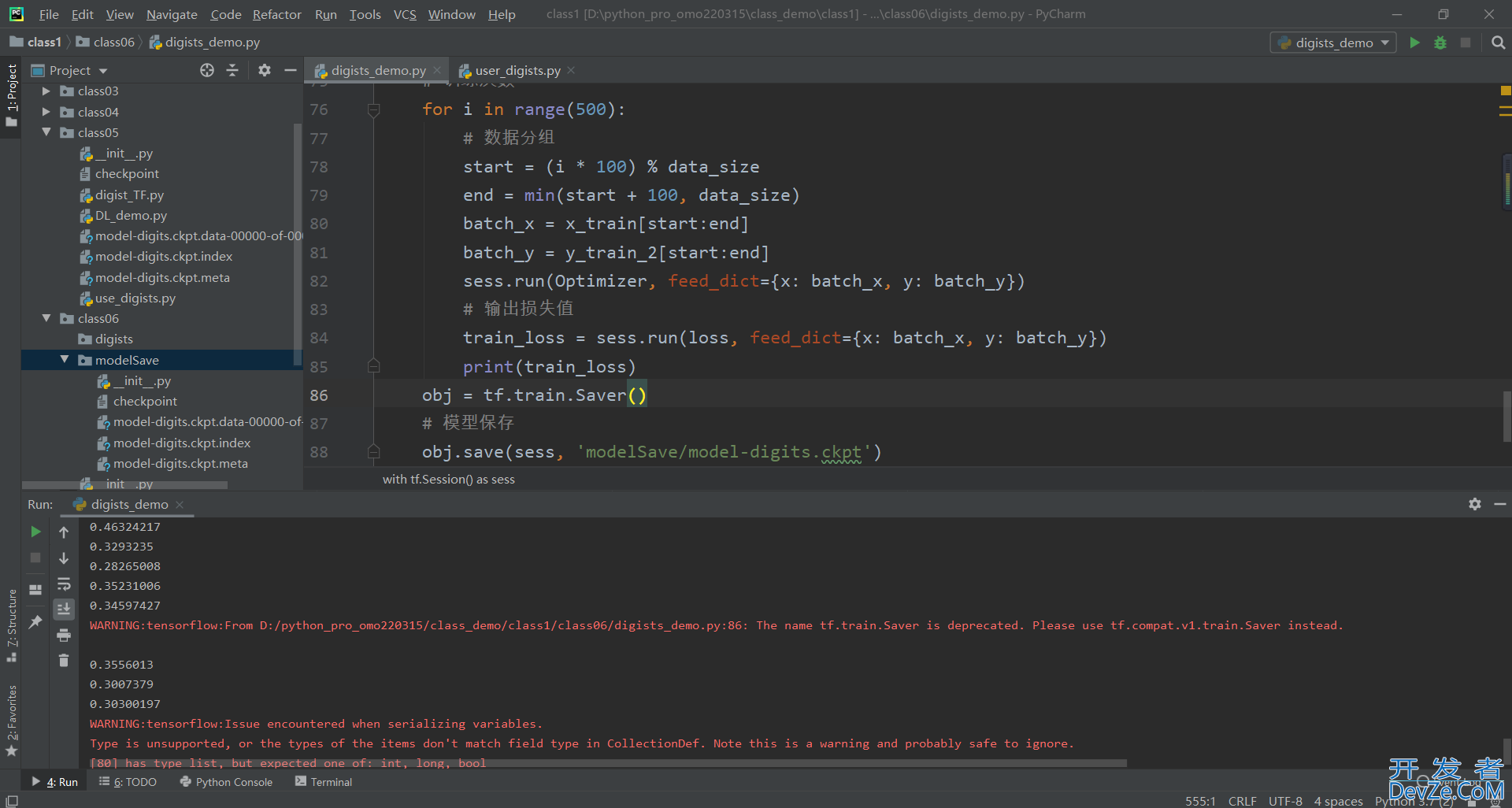
二:手写数字模型使用与测试
对上一步创建的模型,使用测试
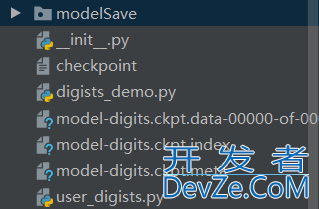
import tensorflow as tf
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# 1加载数据
digits_data = load_digits()
# 数据划分
x_data = digits_data.data
y_data = digits_data.target
# 训练集 + 测试集
x_test = x_data[:40]
y_test = y_data[:40]
x_train = x_data[40:]
y_train = y_data[40:]
# 概率问题
y_train_2 = np.zeros(shape=(len(y_train), 10))
# 对应的分类 当前行对应列变成1
for index, row in enumerate(y_train_2):
# 当前行 对应的数字对应列
row[int(y_train[index])] = 1
# 网络搭建
num_class = 10 # 数字0-9
hidden_num = 80 # 神经元个数
input_size = digits_data.data.shape[1] # 输入的列数
# 数据流图的构建
# x:输入64个特征值--像素
x = tf.placeholder(np.float32, shape=[None, 64])
# y:识别的数字 有几个类别[0-9]
y = tf.placeholder(np.float32, shape=[None, 10])
# 第一层隐藏层
# 参数1 输入维度 参数2:输出维度(神经元个数) 标准差是0.1的正态分布
w1 = tf.Variable(tf.random_normal([input_size, 80], stddev=0.1))
# b的个数就是隐藏层神经元的个数
b1 = tf.Variable(tf.constant(0.01), [80])
# 第一层计算
one = tf.matmul(x, w1) + b1
# 激活函数 和0比 大于0则激活
op1 = tf.nn.relu(one)
# 第二层隐藏层 上一层输出为下一层输入
# 参数1 输入维度 参数2:输出维度(神经元个数) 标准差是0.1的正态分布
w2 = tf.Variable(tf.random_normal([80, 10], stddev=0.1))
# b的个数就是隐藏层神经元的个数
b2 = tf.Variable(tf.constant(0.01), [10])
# 第一层计算
two = tf.matmul(op1, w2) + b2
# 激活函数 和0比 大于0则激活
op2 = tf.nn.relu(two)
# 变量初始化
init = tf.global_variables_initiali编程客栈zer()
train_count = 500
batch_size = 100
data_size = x_train.shape[0]
pre_max_index = tf.argmax(op2, 1)
plt.imshow(digits_data.images[13]) # 3
plt.show()
with tf.Session() as sess:
sess.run(init)
# 使用网络
obj = tf.train.Saver()
obj.restore(sess, 'modelSave/model-digits.ckpt')
print(sess.run(op2, feed_dict={x: [x_test[13], x_test[14]]}))
print(sess.run(pre_max_index, feed_dict={x: [x_test[13], x_test[14]]}))
想要测试的数据,如下图所示

使用模型测试出来的结果,如下图所示,模型基本能够使用
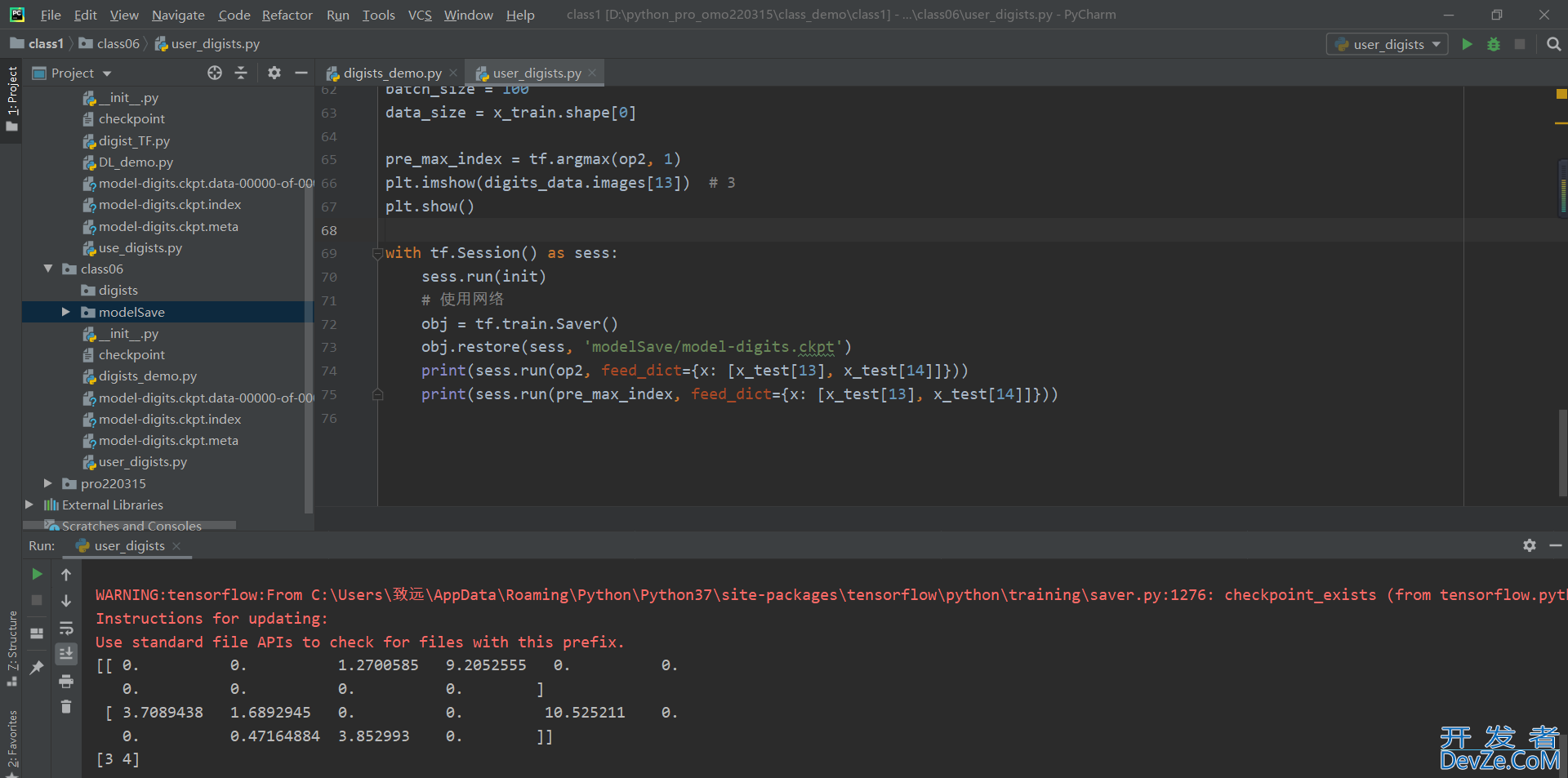
到此这篇关于详解python手写数字识别模型的构建与使用的文章就介绍到这了,更多相关Python手写数字识别模型内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!




 加载中,请稍侯......
加载中,请稍侯......
精彩评论