目录
- 使用工具
- 准备数据
- 转化临界矩阵
- 测试
- 创建图
- 添加节点
- 添加边
- 绘图
- 扩展
- 美化图
- 总结
使用工具
#导入模块 import networkx as nx import numpy as np import matplotlib.pyplot as plt import scipy.sparse as sp
准备数据
# 邻接矩阵
Matrix = np.array(
[
[0, 1, 1, 1, 1, 1, 0, 0], # a
[0, 0, 1, 0, 1, 0, 0, 0], # b
[0, 0, 0, 1, 0, 0, 0, 0], # c
[0, 0, 0, 0, 1, 0, 0, 0], 编程客栈 # d
[0, 0, 0, 0, 0, 1, 0, 0], # e
[0, 0, 1, 0, 0, 0, 1, 1], # f
[0, 0, 0, 0, 0, 1, 0, 1], # g
[0, 0, 0, 0, 0, 1, 1, 0] # h
]
)
转化临界矩阵
def get_matrix_triad(coo_matrix , data=False): ''' 获取矩阵的元组表示 (row,col) data 为 True 时 (row,col,data) :dependent scipy :param coo_matrix: 三元组表示的稀疏矩阵 类型可以为 numpy.ndarray :param data: 是否需要 data值 :return: list ''' # 检查类型 if not sp.isspmatrix_coo(coo_matrix): # 转化为三元组表示的稀疏矩阵 coo_matrix = sp.coo_matrix(coo_编程客栈matrix) # nx3的矩阵 列分别为 矩阵行,矩阵列及对应的矩阵值 temp = np.vstack((coo_matrix.row , coo_matrix.col , coo_matrix.data)).transpose() return temp.tolist()
测试
edags = get_matrix_triad(Matrix) --> [[0.0, 0.0, 1.0], [0.0, 1.0开发者_JS学习, 1.0], [0.0, 2.0, 1.0], [0.0, 3.0, 1.0], [0.0, 4.0, 1.0], [0.0, 5.0, 1.0], [1.0, 1.0, 1.0], [1.0, 2.0, 1.0], [1.0, 4.0, 1.0], [2.0, 2.0, 1.0], [2.0, 3.0, 1.0], [3.0, 3.0, 1.0], [3.0, 4.0, 1.0], [4.0, 4.0, 1.0], [4.0, 5.0, 1.0], [5.0, 2.0, 1.0], [5.0, 5.0, 1.0], [5.0, 6.0, 1.0], [5.0, 7.0, 1.0], [6.0, 5.0, 1.0], [6.0, 6.0, 1.0], [6.0, 7.0, 1.0], [7.0, 5.0, 1.0], [7.0, 6.0, 1.0], [7.0, 7.0, 1.0]]
创建图
# 创建一个没有边,没有节点的空图Graph G = nx.Graph()
添加节点
按照节点的个数添加节点
H = nx.path_graph(Matrix.shape[0]) G.add_nodes_from(H)
添加边
G.add_edges_from(edags) #添加边 # 若数据含有权重,及 get_matrix_triad(http://www.devze.com) 中 data = True ,则使用 G.add_weighted_edges_from(edags)
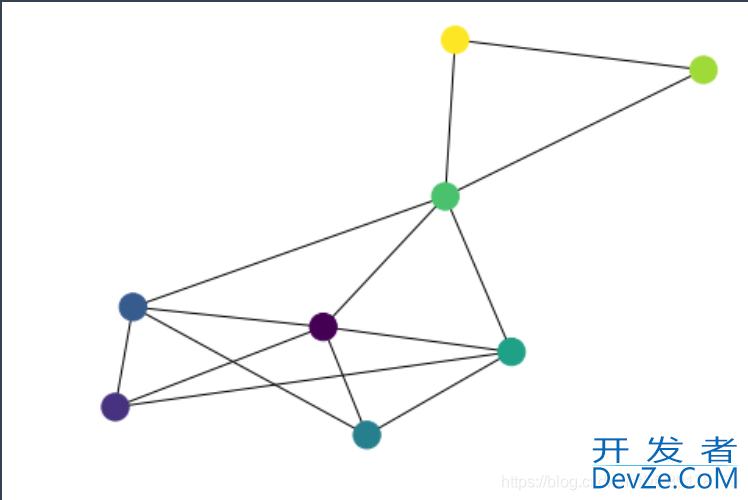
绘图
colors = np.arange(Matrix.shape编程[0]) nx.draw(G,pos=nx.spring_layout(G),node_color=colors) plt.show()
扩展
美化图
合理使用**draw_networkx ()**中的参数,来美化图
draw_networkx()
httpsphp://networkx.github.io/documentation/stable/reference/generated/networkx.drawing.nx_pylab.draw_networkx.html#networkx.drawing.nx_pylab.draw_networkx
总结
以上为个人经验,希望能给大家一个参考,也希望大家多多支持我们。





 加载中,请稍侯......
加载中,请稍侯......
精彩评论