利用Go语言实现二叉搜索树

目录

• 二叉搜索树的特点
• Go 语言实现
• 单元测试

二叉树是一种常见并且非常重要的数据结构，在很多项目中都能看到二叉树的身影。

它有很多变种，比如红黑树，常被用作 std::map 和 std::set 的底层实现；B 树和 B+ 树，广泛应用于数据库系统中。

本文要介绍的二叉搜索树用的也很多，比如在开源项目 go-zero 中，就被用来做路由管理。

这篇文章也算是一篇前导文章，介绍一些必备知识，下一篇再来介绍具体在 go-zero 中的应用。

二叉搜索树的特点

最重要的就是它的有序性，在二叉搜索树中，每个节点的值都大于其左子树中的所有节点的值，并且小于其右子树中的所有节点的值。

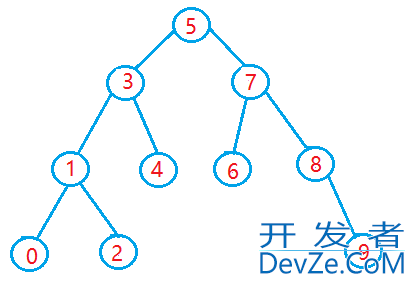
这意味着通过二叉搜索树可以快速实现对数据的查找和插入。

Go 语言实现

本文主要实现了以下几种方法：

• Insert(t)：插入一个节点
• Search(t)：判断节点是否在树中
• InOrderTraverse()：中序遍历
• PreOrderTraverse()：前序遍历
• PostOrderTraverse()：后序遍历
• Min()：返回最小值
• Max()：返回最大值
• Remove(t)：删除一个节点
• String()：打印一个树形结构

下面分别来介绍，首先定义一个节点：

typeNodestruct{
keyint
valuepythonItem
left*Node//left
right*Node//right
}

定义树的结构体，其中包含了锁，是线程安全的：

typeItemBinarySearchTreestruct{
root*Node
locksync.RWMutex
}

插入操作：

func(bst*ItemBinarySearchTree)Insert(keyint,valueItem){
bst.lock.Lock()
deferbst.lock.Unlock()
n:=&Node{key,value,nil,nil}
ifbst.root==nil{
bst.root=n
}else{
insertNode(bst.root,n)
}
}
//internalfunctiontofindthecorrectplaceforanodeinatree
funcinsertNode(node,newNode*Node){
ifnewNode.key<node.key{
ifnode.left==nil{
node.left=newNode
}else{
insertNode(node.left,newNode)
}
}else{
ifnode.right==nil{
node.right=newNode
}else{
insertNode(node.right,newNode)
}
}
}

在插入时，需要判断插入节点和当前节点的大小关系，保证搜索树的有序性。

中序遍历：

func(bst*ItemBinarySearchTree)InOrderTraverse(ffunc(Item)){
bst.lock.RLock()
deferbst.lock.RUnlock()
inOrderTraverse(bst.root,f)
}
//internalrecursivefunctiontotraverseinorder
funcinOrderTraverse(n*N编程ode,ffunc(Item)){
ifn!=nil{
inOrderTraverse(n.left,f)
f(n.value)
inOrderTraverse(n.right,f)
}
}

前序遍历：

func(bst*ItemBinarySearchTree)PreOrderTraverse(ffunc(Item)){
bst.lock.Lock()
deferbst.lock.Unlock()
preOrderTraverse(bst.root,f)
}
//internalrecursivefunctiontotraversepreorder
funcpreOrderTraverse(n*Node,ffunc(Item)){
ifn!=nil{
f(n.value)
preOrderTraverse(n.left,f)
preOrderTraverse(n.right,f)
}
}

后序遍历：

func(bst*ItemBinarySearchTree)PostOrderTraverse(ffunc(Item)){
bst.lock.Lock()
deferbst.lock.Unlock()
postOrderTraverse(bst.root,f)
}
//internalrecursivefunctiontotraversepostorder
funcpostOrderTraverse(n*Node,ffunc(Item)){
ifn!=nil{
postOrderTraverse(n.left,f)
postOrderTraverse(n.right,f)
f(n.value)
}
}

返回最小值：

func(bst*ItemBinarySearchTree)Min()*Item{
bst.lock.RLock()
deferbst.lock.RUnlock()
n:=bst.root
ifn==nil{
returnnil
}
for{
ifn.left==nil{
return&n.value
}
n=n.left
}
}

由于树的有序性，想要得到最小值，一直向左查找就可以了。

返回最大值：

func(bst*ItemBinarySearchTree)Max()*Item{
bst.lock.RLock()
deferbst.lock.RUnlock()
n:=bst.root
ifn==nil{
returnnil
}
for{
ifn.right==nil{
return&n.value
}
n=n.right
}
}

查找节点是否存在：

func(bst*ItemBinarySearchTree)Search(keyint)bool{
bst.lock.RLock()
deferbst.lock.RUnlock()
returnsearch(bst.root,key)
}
//internalrecursivefunctiontosearchaniteminthetree
funcsearch(n*Node,keyint)bool{
ifn==nil{
returnfalse
}
ifkey<n.key{
returnsearch(n.left,key)
}
ifkey>n.key{
returnsearch(n.right,key)
}
returntrue
}

删除节点：

func(bst*ItemBinarySearchTree)Remove(keyint){
bst.lock.Lock()
deferbst.lock.Unlock()
remove(bst.root,key)
}
//internalrecursivefunctiontoremoveanitem
funcremove(node*Node,keyint)*Node{
ifnode==nil{
returnnil
}
ifkey<node.key{
node.left=remove(node.left,key)
returnnode
}
ifkey>node.key{
node.right=remove(node.right,key)
returnnode
}
//key==node.key
ifnode.left==nil&&node.right==nil{
node=nil
returnnil
}
ifnode.left==nil{
node=node.right
returnnode
}
ifnode.right==nil{
node=node.编程left
returnnode
}
leftmostrightside:=node.right
for{
//findsmallestvalueontherightside
ifleftmostrightside!=nil&&leftmostrightside.left!=nil{
leftmostrightside=leftmostrightside.left
}else{
break
}
}
node.key,node.value=leftmostrightside.key,leftmostrightside.value
node.right=remove(node.right,node.key)
returnnode
}

删除操作会复杂一些，分三种情况来考虑：

• 如果要删除的节点没有子节点，只需要直接将父节点中，指向要删除的节点指针置为 nil 即可
• 如果删除的节点只有一个子节点，只需要更新父节点中，指向要删除节点的指针，让它指向删除节点的子节点即可
• 如果删除的节点有两个子节点，我们需要找到这个节点右子树中的最小节点，把它替换到要删除的节点上。然后再删除这个最小节点，因为最小节点肯定没有左子节点，所以可以应用第二种情况删除这个最小节点即可

最后是一个打印树形结构的方法，在实际项目中其实并没有实际作用：

func(bst*ItemBinarySearchTree)String(){
bst.lock.Lock()
deferbst.lock.Unlock()
fmt.Println("------------------------------------------------")
stringify(bst.root,0)
fmt.Println("------------------------------------------------")
}
//internalrecursivefunctiontoprintatree
funcstringify(n*Node,levelint){
ifn!=nil{
format:=""
fori:=0;i<level;i++{
format+=""
}
format+="---["
level++
stringify(n.left,level)
fmt.Printf(format+"%d\n",n.key)
stringify(n.right,level)
}
}

单元测试

下面是一段测试代码：

funcfillTree(bst*ItemBinarySearchTree){
bst.Insert(8,"8")
bst.Insert(4,"4")
bst.Insert(10,"10")
bst.Insert(2,"2")
bst.Insert(6,"6")
bst.Insert(1,"1")
bst.Insert(3,"3")
bst.Insert(5,"5")
bst.Insert(7,"7")
bst.Insert(9,"9")
}
funcTestInsert(t*testing.T){
fillTree(&bst)
bst.String()
bst.Insert(11,"11")
bst.String()
}
//isSameSlicereturnstrueifthe2slicesareidentical
funcisSameSlice(a,b[]string)bool{
ifa==nil&&b==nil{
returntrue
}
ifa==nil||b==nil{
returnfalse
}
iflen(a)!=len(b){
returnfalse
}
fori:=rangea{
ifa[i]!=b[i]{
returnfalse
}
}
returntrue
}
fu编程客栈ncTestInOrderTraverse(t*testing.T){
varresult[]string
bst.InOrdpythonerTraverse(func(iItem){
result=append(result,fmt.Sprintf("%s",i))
})
if!isSameSlice(result,[]string{"1","2","3","4","5","6","7","8","9","10","11"}){
t.Errorf("Traversalorderincorrect,got%v",result)
}
}
funcTestPreOrderTraverse(t*testing.T){
varresult[]string
bst.PreOrderTraverse(func(iItem){
result=append(result,fmt.Sprintf("%s",i))
})
if!isSameSlice(result,[]string{"8","4","2","1","3","6","5","7","10","9","11"}){
t.Errorf("Traversalorderincorrect,got%vinsteadof%v",result,[]string{"8","4","2","1","3","6","5","7","10","9","11"})
}
}
funcTestPostOrderTraverse(t*testing.T){
varresult[]string
bst.PostOrderTraverse(func(iItem){
result=append(result,fmt.Sprintf("%s",i))
})
if!isSameSlice(result,[]string{"1","3","2","5","7","6","4","9","11","10","8"}){
t.Errorf("Traversalorderincorrect,got%vinsteadof%v",result,[]string{"1","3","2","5","7","6","4","9","11","10","8"})
}
}
funcTestMin(t*testing.T){
iffmt.Sprintf("%s",*bst.Min())!="1"{
t.Errorf("minshouldbe1")
}
}
funcTestMax(t*testing.T){
iffmt.Sprintf("%s",*bst.Max())!="11"{
t.Errorf("maxshouldbe11")
}
}
funcTestSearch(t*testing.T){
if!bst.Search(1)||!bst.Search(8)||!bst.Search(11){
t.Errorf("searchnotworking")
}
}
funcTestRemove(t*testing.T){
bst.Remove(1)
iffmt.Sprintf("%s",*bst.Min())!="2"{
t.Errorf("minshouldbe2")
}
}

上文中的全部源码都是经过测试的，可以直接运行，并且已经上传到了 github，需要的同学可以自取。

到此这篇关于利用Go语言实现二叉搜索树的文章就介绍到这了,更多相关Go二叉搜索树内容请搜索编程客栈(www.devze.com)以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程客栈(www.devze.com)！