Java数据结构之位图的简单实现和使用_开发_开发者

1. 什么是位图

位图, 是一种非常常见的结构, 它使用每个二进制位来存放一个值的状态, 就类似于 Java 当中 HashSet 存储元素的功能.

在 Java 当中, 可以使用HashSet完成如下操作:

add(T v): 添加一个元素到 HashSet 中, 重复则覆盖.contains(T v): 判断元素在 HashSet 中是否存在.remove(T v): 从 HashSet 中删除指定元素.

但如果我们的数据范围是固定的, 使用位图就比使用HashSet更省空间, 那么下面就来介绍一下位图如何实现.

在 Java 中, 一个 int 类型的整数是 4 字节, 就可以表示 32 个 bit位, 所以, 如果数据范围是 [0, 31], 就可以直接使用一个 int 类型的空间来完成上述三个操作.

例如:

add(5) 这个操作, 就是在一个 int 类型空间中, 把第 5 个二进制位设置为 1;

Java数据结构之位图的简单实现和使用

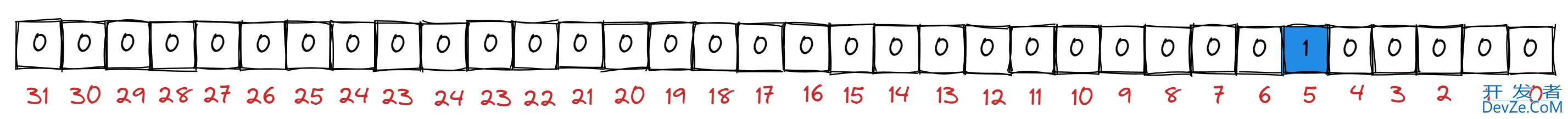
继续执行 add(7) 这个操作, 就是在和上面同一个 int 类型空间中, 把第 7 个二进制位设置为 1;

Java数据结构之位图的简单实现和使用

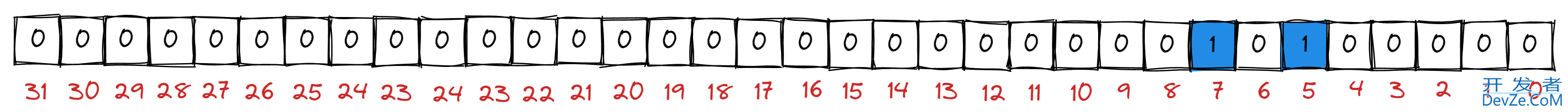
contains(5) 这个操作, 就是判断第5个二进制位是 0 还是 1, 如果是 1, 就说明 4 存在, 如果是 0 , 就说明 4 不存在;

remove(7) 这个操作, 就是把 7 号位置置为 0;

Java数据结构之位图的简单实现和使用

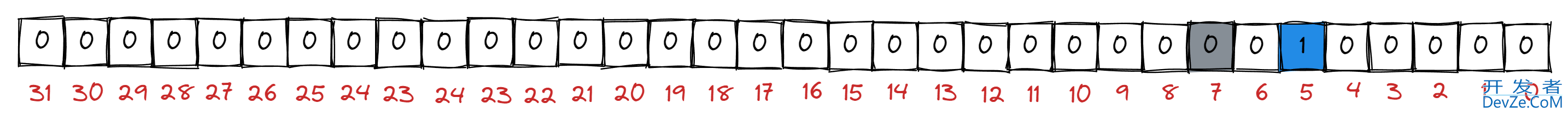
如果数据范围是 0 ~ 1023, 则可以用一个 androidint 类型的数组来表示, 这个数组只需要 32 个元素即可; 因为 32 个 int 类型元素, 可以表示 1024 位, 正好可以覆盖 0 ~ 1023 范围中的所有数字; 对于0 ~ 1023中任意一个数 num, num 在数组中存在第num / 32号下标元素中的第num % 32位中.

例如当 num = 37 时, num 应该在数组 1 号 (即: 37 / 32) 下标的元素的第 5 个 bit (即: 37 % 32) 位上.

Java数据结构之位图的简单实现和使用

2. 位图的简单实现

为了增大位图可以表示的范围, 我们可以使用 long 类型来替代 int 类型, 一个long 类型是 64 个 bit位置, 就可以表示64个数, 下面介绍位图的简单实现, 主要实现上面提到的增, 删, 查三个方法.

首先定义好位图类的大框架, 如下:

public static class BitMap {
    private final long[] bits;

    // 位图初始化
    public BitMap(int max) {
    }

    // 添加一个元素
    public void add(int num) {
    }

    // 删除一个元素
    public void remove(int num) {
    }

    // 判断一个元素是否在位图中
    public boolean contains(int num) {
    }
}

注: 这里只简单考虑非负数存到位图中, 对于负数的情况, 其实也是可以转换成正数来处理的; 比如: -3~6, 可以转换成0~9, 0 就代表 -3, 以此类推, 编程客栈一一对应.

首先是位图的初始化, 要根据数据范围确定位图应该开辟多大的数组空间.

由于我们这里是 long 类型的, 所以, 对于 0 ~ x 范围来说, 就需要准备 (x + 64) / 64 这么大的 long 类型数组.

位图中增加一个元素, 比如我们要增加 53 这个元素, 先定位它是数组中的哪个元素, 即 53 / 64 = 0, 就是在第 0 号下标位置的元素, 再定位是这个元素中的第几个bit位, 即: 53 % 64 = 11, 即第 11 个 bit 位, 我们可以用 1L << 11 后的值与 | 上 bits[0] 即可 (将相应二进制位的值修改为1, 不影响其他位).

代码实现如下:

public void add(int num) {
    bits[num / 64] |= (1L << (num % 64));
}

由于 num / 64其实就是 num >> 6, num % 64其实就是num & 63 (只适用于 2 的 n 次方), 位运算是比算术运算效率要高的, 所以我们可以将 add 方法可以改写成如下形式:

// 向位图中添开发者_Go培训加值, 将对应的二进制位改成1即可
public void add(int num) {
    // 1. num / 64 找到该数应该存在数组的哪个元素上
    // 2. num % 64 找到该数应该存到元素的第几个二进制位置上(从0位置开始)
    // 3. ( 1L << (num % 64) ) | bits[num / 64] 就是将相应二进制位的值修改为1, 不影响其他位
    // 要注意1后面必须加上L, 1默认是一个int类型的数, 是没有64位的, 移位运算就可能会出错
    //  num / 64       1L << (num % 64)
    bits[num >> 6] |= (1L << (num & 63));
}

位图中删除一个元素, 其实就是把对应位置的二进制位修改为 0, 其他位置保持不变, 通过

~(1L << (num & 63));

可以预先得到一个除目标位置是 0, 其他位置都是 1 的数.

然后通过这个数去去 & 数组目标位置的元素, 即可把对应位置的 1 改为 0, 其他位置不变.

// 在集合中删除记录, 将对应二进制位改成0即可
public void remove(int num) {
    // 1. num / 64 找到该数应该存在数组的哪个元素上
    // 2. num % 64 找到该数应该存到元素的第几个二进制位置上(从0位置开始)
    // 3. ~( 1L << (num % 64) ) 就是在把0001000变成1110111这样的
   php // 4. 把 3 得到的结果再 & 到 bits[num >> 6] 就行了
    bits[num >> 6] &= ~(1L << (num & 63));
}

位图中是否包含某个元素, 其实就是判断对应位置是 0 还是 1, 如果是 1, 就说明存在, 如果是 0, 则不存在.

public boolean contains(int num) {
    return (bits[num >> 6] & (1L << (num & 63))) != 0;
}

位图的完整代码见:

// 位图的简单实现
public class BitMap {
    private long[] bits;
    // 传入集合要保存的最大数值
    public BitMap(int max) {
                           // max / 64 + 1
        this.bits = new long[(max >> 6) + 1];
    }
    // 向位图中添加值, 将对应的二进制位改成1即可
    public void add(int num) {
        // 1. num / 64 找到该数应该存在数组的哪个元素上
        // 2. num % 64 找到该数应该存到元素的第几个二进制位置上(从0位置开始)
        // 3. ( 1L << (num % 64) ) | bits[num / 64] 就是将相应二进制位的值修改为1, 不影响其他位
        // 要注意1后面必须加上L, 1默认是一个int类型的数, 是没有64位的, 移位运算就可能会出错
        //  num / 64       1L << (num % 64)
        bits[num >> 6] |= (1L << (num & 63));
    }
    // 在集合中删除记录, 将对应二进制位改成0即可
    public void remove(int num) {
        // 1. num / 64 找到该数应该存在数组的哪个元素上
        // 2. num % 64 找到该数应该存到元素的第几个二进制位置上(从0位置开始)
        // 3. ~( 1L << (num % 64) ) 就是在把0001000变成1110111这样的
        // 4. 把 3 得到的结果再 & 到 bits[num >> 6] 就行了
        bits[num >> 6] &= ~(1L << (num & 63));
    }
    // 查看位图中是否记录了某个值
    public boolean contains(int num) {
        return (bits[num >> 6] & (1L << (num & 63))) != 0;
    }
}

3. 测试位图代码

通过实现的位图和 Java 自带的 HashSet 进行对比着进行测试, 测试代码如下:

import java.util.HashSet;
public class BitMap {
    private long[] bits;
    public BitMap(iphpnt max) {
        bits = new long[(max + 64) >> 6];
    }
    public void add(int num) {
        bits[num >> 6] |= (1L << (num & 63));
    }
    public void remove(int num) {
        bits[num >> 6] &= ~(1L << (num & 63));
    }
    public static void main(String[] args) {
        System.out.println("测试开始!");
        int max = 10000;
        BitMap bitMap = new BitMap(max);
        HashSet<Integer> set = new HashSet<>();
        int testTime = 10000000;
        for (int i = 0; i < testTime; i++) {
            int num = (int) (Math.random() * (max + 1));
            double decide = Math.random();
            if (decide < 0.333) {
                bitMap.add(num);
                set.add(num);
            } else if (decide < 0.666) {
                bitMap.remove(num);
                set.remove(num);
            } else {
                if (bitMap.contains(num) != set.contains(num)) {
                    System.out.println("出错了!");
                    break;
                }
     php       }
        }
        for (int num = 0; num <= max; num++) {
            if (bitMap.contains(num) != set.contains(num)) {
                System.out.println("出错了!");
            }
        }
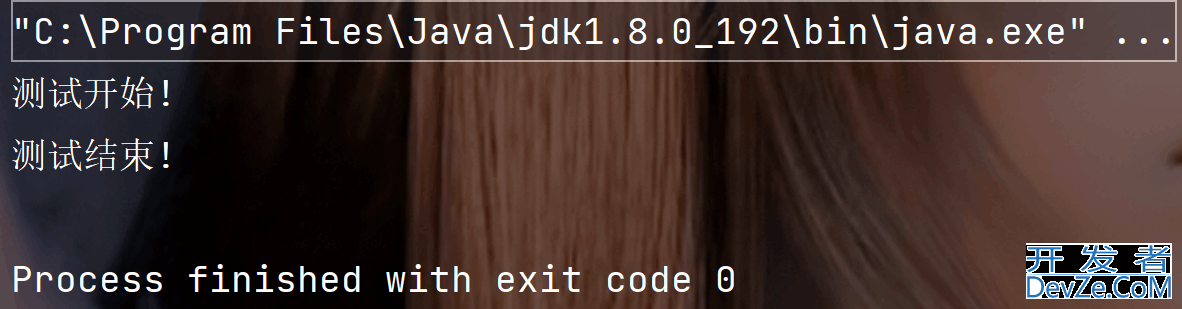
        System.out.println("测试结束!");
    }
}

执行代码, 可以看到看到结果中是没有打印错错误信息的, 所以上面位图的逻辑实现是正确的.

Java数据结构之位图的简单实现和使用