NumPy之矩阵向量线性代数等操作示例

目录

• NumPy矩阵和向量
• 矩阵
• 向量
• 创建向量
• 创建矩阵
• 访问元素
• 转置矩阵
• 矩阵加减乘除
• 矩阵向量乘法
• 矩阵求逆
• 矩阵的迹
• 向量点积
• 向量范数
• NumPy线性代数
• 计算矩阵乘积
• 计算矩阵的逆
• 解线性方程组

NumPy矩阵和向量编程客栈

矩阵

在NumPy中，矩阵可以python看作是一个二维数组，其中每个元素都可以通过行列坐标来定位。它表示为一个m×n的矩形网格，其中m表示矩阵的行数，n表示矩阵的列数。在计算机科学中，矩阵通常用数字或符号表示，并且可以进行加、减、乘等运算。

一个M X N的矩阵python是一个由M行（row）N列（column）元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或数学式。

以下是一个由 6 个数字元素构成的 2 行 3 列的矩阵：

[1 2 3]
[4 5 6]

注意：2×3矩阵即2行3列，请把左、右两边的多个[与多个]看成一个整体[]

向量

在 NumPy 中，向量是一维数组对象，其所有元素都必须具有相同的数据类型。向量可以通过创建一个一维数组来实现。

向量是一种特殊的矩阵，其中只包含一行或一列元素。向量通常用数字或符号表示，其大小表示向量包含的元素数量。

创建一个包含五个元素的向量：

import numpy as np
v = np.array([1, 2, 3, 4, 5])

创建向量

import numpy as np
# 创建一维数组
v = np.array([1, 2, 3])
print(v)  # 输出：[1 2 3]

创建矩阵

import numpy as np
# 创建二维数组
m = np.array([[1, 2, 3], [4, 5, 6]])
print(m)  # 输出：[[1 2 3]
          #      [4 5 6]]

访问元素

import numpy as np
# 创建一维数组
v = np.array([1, 2, 3])
# 访问元素
print(v[0])  # 输出：1
print(v[1])  # 输出：2
print(v[2])  # 输出：3

转置矩阵

NumPy中除了可以使用numpy.transpose 函数来对换数组的维度，还可以使用 T 属性。

例如有个 m 行 n 列的矩阵，使用 t() 函数就能转换为 n 行 m 列的矩阵。

import numpy as np
# 创建矩阵
A = np.array([[1, 2], [3, 4]])
# 转置矩阵
AT = np.transpose(A)
print(AT)  # 输出：[[1 3]
           #      [2 4]]
print (A.T)    

矩阵加减乘除

# 矩阵加法
np.add(A, B)
# 矩阵减法
np.subtract(A, B)
# 矩阵乘法
# 在进行矩阵乘法时，前一个矩阵的列数必须等于后一个矩阵的行数，才能进行乘法运算
# (M行, N列)*(N行, L列) = (M行, L列)
p.dot(A, B)
# 矩阵除法
np.divide(A, B)

import numpy as np
# 创建矩阵A和B
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print("A + B:")
print(np.add(A, B))
[1, 2]  	[5, 6]		[6, 8]
		+  			=  
[3, 4]		[7, 8]		[10, 12]
print("A - B:")
print(np.subtract(A, B))
[1, 2]  	[5, 6]		[-4, -4]
		-  			=  
[3, 4]		[7, 8]		[-4, -4]
print("A * B:")
print(np.dot(A, B))
[1, 2]  	[5, 6]		[19, 22]
		*  			=  
[3, 4]		[7, 8]		 [43, 50]
print("A / B:")
print(np.divide(A, B))
[1, 2]  	[5, 6]		[0.2,  0.33333333]
		/  			=  
[3, 4]		[7, 8]		[0.42857143, 0.5]

矩阵和矩阵(向量)相乘： (M行, N列)*(N行, L列) = (M行, L列)

矩阵向量乘法

m×n 的矩阵乘以 n×1 的向量，得到的是 m×1 的向量

[1, 2]  	[1]			[19]
		*  			=  
[3, 4]		[1]			 [43]

矩阵求逆

使用numpy.linalg.inv()函数进行矩阵求逆操作

import numpy as np
# 创建矩阵
matrix = np.array([[1, 2], [3, 4]])
# 求逆矩阵
result = np.linal编程客栈g.inv(matrix)
print(result)

矩阵的迹

使用numpy.trace()函数可以计算矩阵的迹

import numpy as np
# 创建矩阵
matrix = np.array([[1,编程客栈 2], [3, 4]])
# 计算矩阵的迹
result = np.trace(matrix)
print(result)

向量点积

使用numpy.dot()函数进行向量点积操作

import numpy as np
# 创建两个向量
vector1 = np.array([1, 2])
vector2 = np.array([3, 4])
# 向量点积
result = np.dot(vector1, vector2)
print(result)

向量范数

使用numpy.linalg.norm()函数可以计算向量的范数

import numpy as np
# 创建向量
vector = np.array([1, 2, 3])
# 计算向量的L2范数
result = np.linalg.norm(vector)
print(result)

NumPy线性代数

NumPy的线性代数模块（numpy.linalg）提供了许多矩阵运算函数，如矩阵乘法、求逆、行列式、特征值等，该库包含了线性代数所需的所有功能。

常用的 NumPy 线性代数函数：

函数	说明
np.dot(a, b)：	两个数组的点积，即元素对应相乘
np.matmul(a, b)	两个数组的矩阵积
np.linalg.inv(a)	计算矩阵的逆
np.linalg.det(a)	计算矩阵的行列式
np.linalg.eig(a)	计算矩阵的特征值和特征向量
np.linalg.solve(a, b)	解线性方程组 ax=b

计算矩阵乘积

开发者_Python教程

import numpy as np
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
print(np.dot(a, b))
# [[19 22]
#  [43 50]]

计算矩阵的逆

import numpy as np
a = np.array([[1, 2], [3, 4]])
print(np.linalg.inv(a))
# [[-2.   1. ]
#  [ 1.5 -0.5]]

解线性方程组

import numpy as np
a = np.array([[2, 3], [4, 5]])
b = np.array([5, 6])
x = np.linalg.solve(a, b)
print(x) # [-4.  5.]

解得的线性方程组如下，其解为x1=−4，x2=5

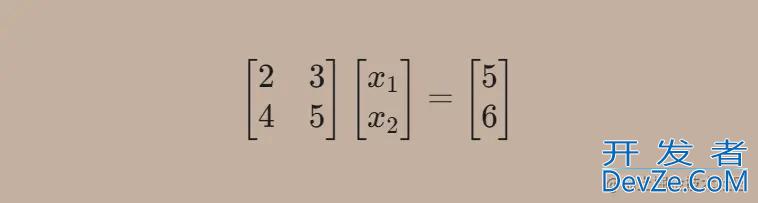
以上就是NumPy之矩阵向量线性代数等操作示例的详细内容，更多关于NumPy 矩阵向量线性代数的资料请关注我们其它相关文章！