目录
- 1.二叉树的遍历
- 1.1前序遍历
- 1.2中序遍历
- 1.3后序遍历
- 1.4层次遍历
- 2.链式二叉树的实现
- 2.1二叉树的创建
- 2.2前序遍历
- 2.3中序遍历
- 2.4后序遍历
- 2.5层序遍历
- 2.6销毁
- 2.7求节点个数
- 2.8求叶子节点个数
- 2.9求二叉树的深度
- 2.10求第K层节点个数
- 2.11查找
- 2.12判断是否为完全二叉树
1.二叉树的遍历
所谓二叉树遍历 (Traversal) 是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。 访问结点所做的操作依赖于具体的应用问题。遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历分为: 前序遍历、中序遍历、后序遍历的递归遍历,层序遍历的非递归遍历下面将以下面的二叉树为例讲解四种遍历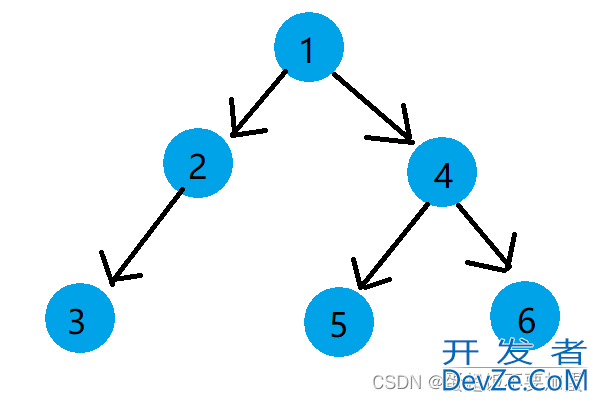
1.1前序遍历
二叉树的前序遍历也叫先序遍历,遍历的顺序为:根、左子树、右子树,即遇到一棵树,先访问根节点,再访问左子树和右子树,访问左子树和右子树的过程又分为先访问根节点,再访问左子树和右子树,这是一个递归访问的过程,因此前序遍历属于递归遍历
遍历的过程将以文字和图片两种方式展现

遍历过程:
先遇到根节点1,访问根节点1,再访问1的左子树
1的左子树:遇到根节点2,访问根节点2,再访问2的左子树,2的左子树只有一个根节点3,3的左右子树为空因此不需要访问3的左右子树,访问根节点3便结束,2的左子树遍历结束访问2的右子树,2的右子树为空即不用访问,此时2的整颗树遍历结束,即1的左子树遍历结束,然后接着访问1的右子树
1的右子树:遇到根节点4,访问根节点4,再访问4的左子树,4的左子树只有一个根节点5,5的左右子树为空因此不需要访问5的左右子树,访问根节点5便结束,4的左子树遍历结束访问4的右子树,4的右子树只有一个根节点6,6的左右子树为空因此不需要访问6的左右子树,访问根节点6便结束,此时4的整颗树遍历结束,即1的右子树遍历结束
整棵树遍历完成,遍历序列为:1 2 3 4 5 6
遍历图示:
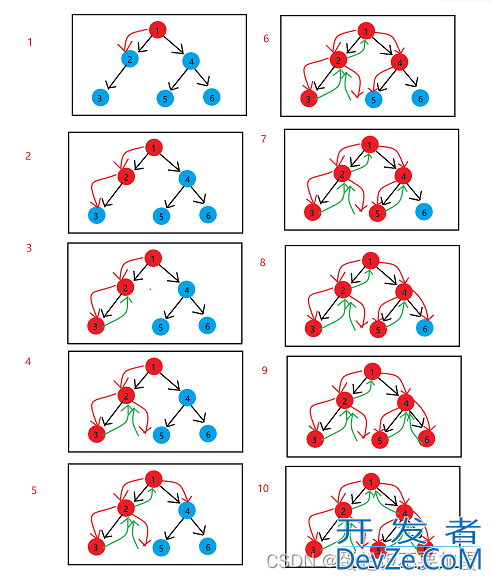
1.2中序遍历
二叉树的中序遍历也叫中根遍历,遍历的顺序为:左子树、根、右节点,即遇到一棵树,先访问它的左子树,再访问根,最后访问右子树,访问左子树和右子树的过程又分为先访问左子树,再访问根和右子树,这是一个递归访问的过程,因此中序遍历也属于递归遍历
遍历的过程将以文字和图片两种方式展现

遍历过程:
遇到根节点1,先不访问根节点,先访问1的左子树
1的左子树:遇到根节点2,先不访问根节点2,先访问2的左子树:2的左子树只有一个根节点3,3的左右子树为空因此不需要访问3的左右子树,访问根节点3便结束,此时2的左子树结束,访问根节点2,然后访问2的右子树,2的右子树为空则不访问,此时2的整颗树遍历结束,即1的左子树遍历结束
访问根节点1,接着访问1的右子树
1的右子树:遇到根节点4,先不访问根节点4,先访问4的左子树:遇到根节点5,5的左右子树为空因此不需要访问5的左右子树,访问根节点5便结束,此时4的左子树访问结束,访问根节点4,接着访问4的右子树,4的右子树只有一个根节点6,6的左右子树为空因此不需要访问6的左右子树,访问根节点6便结束,此时4的整棵树访问结束,即1的右子树访问结束
整棵树遍历完成,遍历序列:3 2 1 5 4 6
遍历图示:

1.3后序遍历
二叉树的后序遍历也叫后根遍历,遍历的顺序为:左子树、右子树、根,即遇到一棵树,先访问它的左子树,再访问右子树,最后访问根,访问左子树和右子树的过程又分为先访问左子树,再访问右子树和根,这是一个递归访问的过程,因此后序遍历也属于递归遍历
遍历的过程将以文字和图片两种方式展现

遍历过程:
遇到根节点1,先不访问根节点1,先访问左子树
1的左子树:遇到根节点2,先不访问根节点2,先访问2的左子树:2的左子树只有根节点3,3的左右子树为空因此不需要访问3的左右子树,访问根节点3便结束,此时2的左子树访问结束,接着访问2的右子树,2的右子树为空因此不需要访问,此时2的左右子树访问结束,最后访问根节点2,此时2的整颗树访问结束,即1的左子树访问结束,接着访问1的右子树
1的右子树:遇到根节点4,先不访问根节点4,先访问4的左子树:5的左右子树为空因此不需要访问5的左右子树,访问根节点5便结束,此时4的左子树访问结束,接着访问4的右子树,6的左右子树为空因此不需要访问6的左右子树,访问根节点6便结束,此时4的左右子树遍历结束,最后访问根节点4,4的整颗树访问结束,即1的右子树访问结束
最后访问根节点1,整棵树遍历结束,遍历序列:3 2 5 6 4 1
遍历图示:
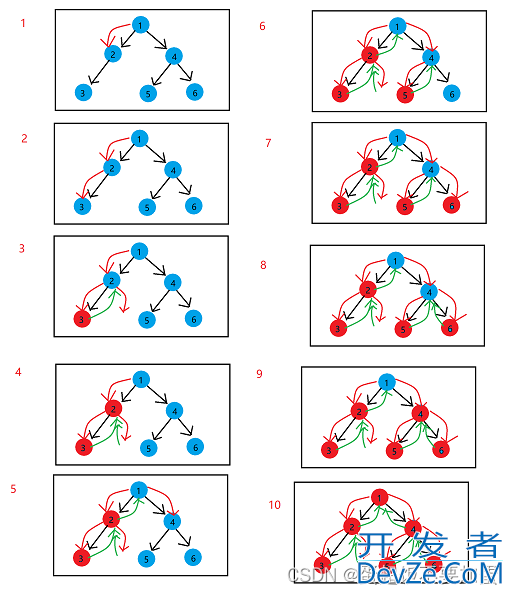
1.4层次遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1, 层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第 2 层上的节点,接着是第三层的节点,以此类推, 自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
遍历图示:
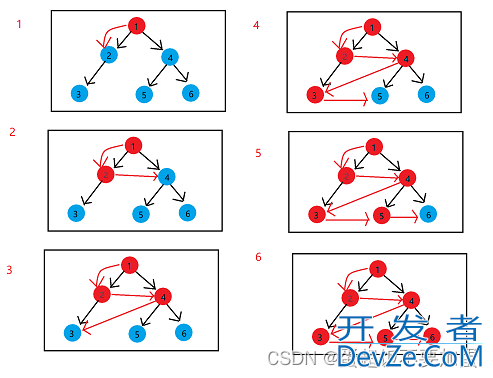
由上图可以看出,层序遍历为非递归遍历
2.链式二叉树的实现
链式二叉树的实现包括二叉树的创建、遍历、销毁、求节点个数、求叶子节点个数、求二叉树的深度、求第k层节点个数、查找、判断是否是完全二叉树等
下面我们一一来实现这些接口
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
开发者_Python学习2.1二叉树的创建
给定一个前序遍历字符串,按照此字符串以指针方式构建一颗二叉树
给定字符串ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树
代码设计思路:
函数参数为字符串指针和下标指针,利用递归的思想,首先判断是否遇到空格,遇到空格则跳过该空格即下标加1并返回,接着构建一个节点,当前字符指针指向的字符赋值给节点的值域然后下标加1,将字符指针和下标传参调用递归函数然后用节点的左指针接收。再将字符指针和下标传参调用递归函数然后用节点的右指针接收,最后返回节点指针
BTNode *TreeBuild(char *arr,int* i)
{
if(arr[*i]=='#')//遇到空格则跳过该空格
{
(*i)++;
return NULL;
}
// 建立节点
BTNode *root=(BTNode *)malloc(sizeof(BTNode));
//节点的值为当前下标指向的字符
rot->data=arr[(*i)++];
//调用递归,并用节点的左指针接收
root->left=TreeBuild(arr,i);
//调用递归,并用节点的左指针接收
root->right=TreeBuild(arr,i);
return root;
}
2.2前序遍历
前序遍历的过程在前面已经介绍,我们按照过程设计相应的函数
代码设计思路:
利用递归的思想,首先判断当前节点是否为空,为空则直接返回,先打印当前节点的值,再将自己的左子树作为参数调用递归遍历,最后将自己的右子树作为参数调用递归遍历
代码:
void PreOwww.devze.comrder(BTNode* root)
{
if (root == NULL)//当前节点为空则直接返回
return NULL;
printf("%d ", root->data);//打印当前节点的值
PreOrder(root->left);//递归遍历左子树
PreOrder(root->right);//递归调用右子树
}
2.3中序遍历
中序遍历的过程在前面已经介绍,我们按照过程设计相应的函数
代码设计思路:
利用递归的思想,首先判断当前节点是否为空,为空则直接返回,先将自己的左子树作为参数调用递归遍历,再打印当前节点的值,最后将自己的右子树作为参数调用递归遍历
代码:
void InOrder(BTNode* root)
{
if (root == NULL)//当前节点为空则直接返回
return NULL;
InOrder(root->left);//递归遍历左子树
printf("%d ", root->data);//打印当前节点的值
InOrder(root->right);//递归调用右子树
}
2.4后序遍历
后序遍历的过程在前面已经介绍,我们按照过程设计相应的函数
代码设计思路:
利用递归的思想,首先判断当前节点是否为空,为空则直接返回,先将自己的左子树作为参数调用递归遍历,再将自己的右子树作为参数调用递归遍历,最后打印当前节点的值
void PostOrder(BTNode* root)
{
if (root == NULL)//当前节点为空则直接返回
return NULL;
PostOrder(root->left);//递归遍历左子树
PostOrder(root->right);//递归调用右子树
printf("%d ", root->data);//打印当前节点的值
}
2.5层序遍历
层序遍历的过程在前面已经介绍,我们按照过程设计相应的函数
代码设计思路:
利用队列,首先判断当前节点是否为空,为空则直接返回。把第一个节点的指针入队,然后进去循环(循环条件是队列不为空),定义一个指针拿到队列的第一个节点,然后出队并打印节点的值,出队之后将节点的左右孩子入队,如果节点的左孩子存在,则将左孩子指针入队,如果节点的右孩子存在,则将右孩子指针入队,然后又继续取队头元素打印,直到队列为空
代码:
void LevelOrder(BTNode *root)
{
Queue q;//定义一个队列
QueueInit(&q);//队列初始化
if (root == NULL)//当前节点为空则返回
return;
QueuePush(&q, root);//将第一个节点指针入队
while (!(QueueEmpty(&q)))//循环条件是队列不为空,队列为空则结束
{
BTNode* front = QueueFront(&q);//取队头节点
printf("%d ", front->data);//打印节点的值
QueuePop(&q);//出队
if (front->left)//左孩子存在,则将左孩子指针入队
{
QueuePush(&q, front->left);
}
if (front->right)//右孩子存在,则将右孩子指针入队
{
QueuePush(&q, front->right);
}
}
QueueDestroy(&q);//销毁队列
}
2.6销毁
销毁的过程:先从最后一层开始销毁,先销毁左子树,再销毁右子树,最后销毁根,即用到后序遍历的思想,递归销毁
代码设计思路:
php利用后序遍历的思想,首先判断当前节点是否为空,为空则返回。先将左孩子指针作为参数调用递归,再将左孩子指针作为参数调用递归,最后将根节点释放
代码:
void BinaryTreeDestory(BTNode* root)
{
if(root == NULL)//为空则返回
return;
BinaryTreeDestory(root->left);//递归销毁左子树
BinaryTreeDestory(root->right);//递归销毁右子树
free(root);//最后销毁根节点
}
2.7求节点个数
一颗树的节点个数可以分为左子树的节点数加上右子树的节点数再加1即根节点,同样是递归求节点个数
代码设计思路:
利用递归的思想,首先判断当前节点是否为空,为空则返回0,然后将左孩子指针作为参数调用递归,再将右孩子指针作为参数调用递归,最后将两者的值加1返回,即节点个数等于左子树的节点个数+右子树的节点个数+1
代码:
int TreeSize(BTNode* root)
{
if (root == NULL)//当前节点为空则返回0
return 0;
//递归左子树和右子树,然后将两者的和加1返回
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
2.8求叶子节点个数
一颗树的叶子节点个数可以分为左子树的叶子节点个数+右子树的叶子节点个数,即同样利用递归求叶子节点个数
代码设计思路:
利用递归的思想,首先判断当前节点是否为空,为空则返回0,然后判断当前节点是否为叶子结点,左孩子和右孩子都为空的节点即为叶子节点,为叶子节点则返回1,接着递归左子树和右子树,并返回两者的和
代码:
int TreeLeafSize(BTNode* root)
{
if (root ==NULL)//当前节点为空则返回0
return 0;
if (root->left == NULL && root->right == NULL)//当前节点为叶子结点则返回1
return 1;
//递归左子树和右子树,并返回两者的和
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
2.JjVtXr9求二叉树的深度
一颗树的深度等于左右子树的较大的深度加1(加根节点),即利用递归求左右子树的深度,将左右子树较大的深度加1返回
代码设计思路:
利用递归的思想,首先判断当前节点是否为空,为空则返回0,再判断当前节点是否为叶节点,是叶节点则返回1,接着递归左子树和右子树,取较大的深度加1返回
代码:
int TreeHeight(BTNode* root)
{
if (root == NULL)//当前节点为空则返回空
return 0;
if (root->left == NULL && root->right == NULL)//当前节点为叶节点则返回1
return 1;
int left = TreeHeight(root->left);//递归左子树
int right = TreeHeight(root->right);//递归右子树
return left > right ? left + 1 : right + 1;//将左右子树较大的深度加1返回
}
2.10求第K层节点个数
整颗树的第k层可以看成第二层的第k-1层,第三层的k-2层,第k层的第1层,即整棵树的第k层的节点数等于左右子树的第k-1层节点子树,即利用递归求左右子树的k-1层节点个数
代码设计思路:
利用递归的思想,首先判断当前节点是否为空,为空则返回0,再判断当前层数是否为1,为1则返回1,然后递归左子树,传左子树指针和k-1,然后递归右子树,传右子树指针和k-1,最后返回两者的和
代码:
int TreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)//当前节点为空则返回0
return 0;
if (k == 1)//当前层数为1则返回1
return 1;
//递归左子树和右子树,返回两者的值
return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}
2.11查找
查找值为x的节点,并返回节点的指针
代码设计思编程客栈路:
利用递归的思想,首先判断当前节点是否为空,为空则返回空,不为空则判断当前节点的值是否等于x,等于则返回该节点,然后递归查找左子树,如果递归左子树返回的值不为空说明找到则返回该值,接着递归右子树,如果递归右子树返回的值不为空说明找到则返回该值,递归左右子树都未找到说明x不存在,返回空
代码:
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)//当前节点为空则返回空
return NULL;
if (root->data == x)//当前节点的值等于x则返回该节点
return root;
//递归左子树查找
BTNode* left = BinaryTreeFind(root->left,x);
//返回的值不为空说明已找到,返回该值
if (left)
return left;
//递归右子树查找
BTNode* right = BinaryTreeFind(root->right, x);
//返回的值不为空说明已找到,返回该值
if (right)
return right;
//递归左右子树均为找到,则赶回空
return NULL;
}
2.12判断是否为完全二叉树
上一篇文章介绍了完全二叉树的概念,完全二叉树可以看成是满二叉树以最后一层开始从右往左挖去了几个节点而成,即完全二叉树的倒数第二层是满的,倒数第一层不可能存在只有右孩子而没有左孩子的情况
代码设计思路:
类似于层序遍历的思想,利用队列,首先判断第一个节点是否为空,为空则返回,然后将第一个节点入队,接着进入循环(循环条件为队列不为空),取队头元素并出队,如果取到的队头元素为空,说明此时已经此时二叉树刚好遍历结束,则退出循环检查后面队列值地情况如果是完全二叉树,则队列后面应该都是空,如果存在不为空的元素则证明不是完全二叉树。如果取到的队头元素不为空,则将其左右孩子(为空也一样)入队,如果循环正常结束,则证明是完全二叉树
代码:
bool BinaryTreeComplete(BTNode* root)
{
Queue q;//定义一个队列
QueueInit(&q);//队列初始化
if (root == NULL)//当前节点为空则返回
return;
QueuePush(&q, root);//将第一个节点入队
while (!(QueueEmpty(&q)))
{
//取队头元素并出队
BTNode* front = QueueFront(&q);
QueuePop(&q);
//取到的队头元素为空则退出循环,检查队列后面值地情况
if (front==NULL)
{
break;
}
else//不为空则将左右孩子入队
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
//检查队列后面的值的情况
while (!(QueueEmpty(&q)))
{
BTNode* front = QueueFront(&q);//取队头元素并出队
QueuePop(&q);
if (front != NULL)//如果有不为空的元素则证明不是完android全二叉树
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);//销毁队列
return true;//循环正常结束则返回true
}
好啦,关于链式二叉树就先学到这里,如果对您有所帮助,欢迎一键三连~
到此这篇关于数据结构之链式二叉树详解的文章就介绍到这了,更多相关C语言 链式二叉树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!





 加载中,请稍侯......
加载中,请稍侯......
精彩评论