y = wx +b
通过meshgrid 得到两个二维矩阵关键理解:plot_surface需要的xyz是二维np数组这里提前准备meshgrid来生产x和y需要的参数下图的W和I即plot_surface需要xy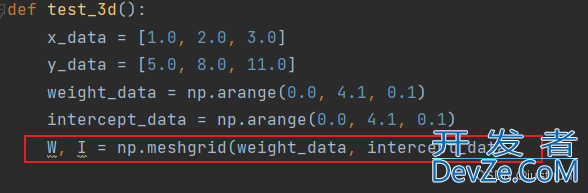
Z即我们需要的权重损失
计算方式要和W,I. I的每行中内容是一样的就是y=wx+b的b是一样的 fig = plt.figure()
ax = fig.add_axes(Axes3D(fig))
ax.plot_surface(W, I, Z=MSE_data)
总的实验代码
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
class LinearModel:
@staticmethod
def forward(w, x):
return w * x
@staticmethod
def开发者_C开发 forward_with_intercept(w, x, b):
return w * x + b
@staticmethod
def get_loss(w, x, y_origin, exp=2, b=None):
if b:
y = LinearModel.forward_with_intercept(w, x, b)
else:
y = LinearModel.forward(w, x)
return pow(y_origin - y, exp)
def test_www.devze.com2d():
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
weight_data = []
MSE_data = []
# 设定实验的权重范围
for w in np.arange(0.0, 4.1, 0.1):
weight_data.append(w)
loss_total = 0
# 计算每个权重在数据集上的MSE平均平方方差
for x_val, y_val in zip(x_data, y_data):
loss_total += LinearModel.get_loss(w, x_val, y_val)
MSE_data.append(loss_total / len(x_data))
编程客栈 php # 绘图
plt.xlabel("weight")
plt.ylabel("MSE")
plt.plot(weight_data, MSE_data)
plt.show()
def test_3d():
x_data = [1.0, 2.0, 3.0]
y_data = [5.0, 8.0, 11.0]
weight_data = np.arange(0.0, 4.1, 0.1)
intercept_data = np.arange(0.0, 4.1, 0.1)
W, I = np.meshgrid(weight_data, intercept_data)
MSE_data = []
# 设定实验的权重范围 循环要先写截距的 meshgrid 的返回第二个是相当于41*41 同一行值相同 ,要在第二层循环去遍历权重
for intercept in intercept_data:
MSE_data_tmp = []
for w in weight_data:
loss_total = 0
# 计算每个权重在数据集上的MSE平均平方方差
for x_val, y_val in zip(x_data, y_data):
loss_total += LinearModel.get_loss(w, x_val, y_val, b=intercept)
MSE_data_tmp.append(loss_total / len(x_data))
MSE_data.append(MSE_data_tmp)
MSE_data = np.array(MSE_data)
fig = plt.figure()
ax = fig.add_axes(Axespython3D(fig))
ax.plot_surface(W, I, Z=MSE_data)
plt.xlabel("weight")
plt.ylabel("intercept")
pwww.devze.comlt.show()
if __name__ == '__main__':
test_2d()
test_3d()
到此这篇关于pytorch实践线性模型3d的文章就介绍到这了,更多相关pytorch线性模型内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!





 加载中,请稍侯......
加载中,请稍侯......
精彩评论