目录
- 前言
- 函数中的 return
- 递归的问题
- 总结
前言
本篇文章主要是记录一下在 GScript 中实现递归调用时所遇到的坑,类似的问题在中文互联网上我几乎没有找到相关的内容,所以还是很有必要记录一下。
在开始htSIqQw开发者_C教程ulT之前还是简单介绍下本次更新的 GScript v0.0.9 所包含的内容:
- 支持可变参数
- 优化
append函数语义 - 优化编译错误信息
- 最后一个就是支持递归调用
先看第一个可变参数:
//formats according to a format specifier and writes to standard output.
printf(string format, any ...a){}
//formats according to a format specifier and returns the resulting string.
string sprintf(string format, a编程客栈ny ...a){}
以上是随着本次更新新增的两个标准函数,均支持可变参数,其中使用 ... 表示可变参数,调用时如下:
printf("hello %s ","123");
printf("hello-%s-%s ","123","abc");
printf("hello-%s-%d ","123",123);
string format = "this is %s ";
printf(format, "gscript");
string s = sprintf("nice to meet %s", "you");
assertEqual(s,"nice to meet you");
与大部分语言类似,可变参数本质上就是一个数组,所以可以拿来循环遍历:
int add(string s, int ...num){
println(s);
int sum = 0;
for(int i=0;i<len(num);i++){
int v = num[i];
sum = sum+v;
}
return sum;
}
int x = add("abc", 1,2,3,4);
println(x);
assertEqual(x, 10);
// appends "v" to the end of a array "a"
append(any[] a, any v){}
之后是优化了内置函数 append() 的语义,本次优化来自于 issue12 的建议: github.com/crossoverJi…
// Before
int[] a={1,2,3};
println(a);
println();
a = append(a,4);
println(a);
// Output: [1 2 3 4]
// Now
int[] a={1,2,3};
println(a);
println();
append(a,4);
int b = a[3];
assertEqual(4, b);
println(a);
// Output: [1 2 3 4]
现在 append 之后不需要再重新赋值,也会追加数据,优化后这里看起来是一个值/引用传递的问题,但其实底层也是值传递,只是在语法上增加了这样的语法糖,帮使用者重新做了一次赋值。
之后是新增了编译错误信息提示,比如下面这段代码:
a+2; b编程+c;
使用没有声明的变量,现在会直接编译失败:
1:0: undefined: a 2:0: undefined: b 2:2: undefined: c
class T{}
class T{}
// output:
2:0: class T redeclared in this blojsck
重复声明之类的语法错误也有相关提示。
最后一个才是本次讨论的重点,也就是递归函数的支持。
int num(int x,int y){
if (y==1 || y ==x) {
return 1;
}
int v1 = num(x - 1, y - 1);
return c;
}
再上一个版本中 int v1 = num(x - 1, y - 1); 这行代码是不会执行的,具体原因后文会分析。
现在利用递归便可以实现类似于打印杨辉三角之类的程序了:
int num(int x,int y){
if (y==1 || y ==x) {
return 1;www.devze.com
}
int v1 = num(x - 1, y - 1);
int v2 = num(x - 1, y);
int c = v1+v2;
// int c = num(x - 1, y - 1)+num(x - 1, y);
return c;
}
printTriangle(int row){
for (int i = 1; i <= row; i++) {
for (int j = 1; j <= row - i; j++) {
print(" ");
}
for (int j = 1; j <= i; j++) {
print(num(i, j) + " ");
}
println("");
}
}
printTriangle(7);
// output:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
函数中的 return
int num(int x,int y){
if (y==1 || y ==x) {
return 1;
}
int v1 = num(x - 1, y - 1);
return c;
}
现在我们来看看这样的代码为什么执行完 return 1 之后就不会执行后边的语句了。
其实在此之前我首先解决的时候函数 return 后不能执行后续 statement 的需求,其实正好就是上文提到的逻辑,只是这里是递归而已。
先把代码简化一下方便分析:
int f1(int a){
if (a==10){
return 10;
}
println("abc");
}
当参数 a 等于 10 的时候确实不能执行后续的打印语句了,那么如何实现该需求呢?
以正常人类的思考方式:当我们执行完 return 语句的时候,就应该标记该语句所属的函数直接返回,不能在执行后续的 statement。
可是这应该如何实操呢?
其实看看 AST 就能明白了:
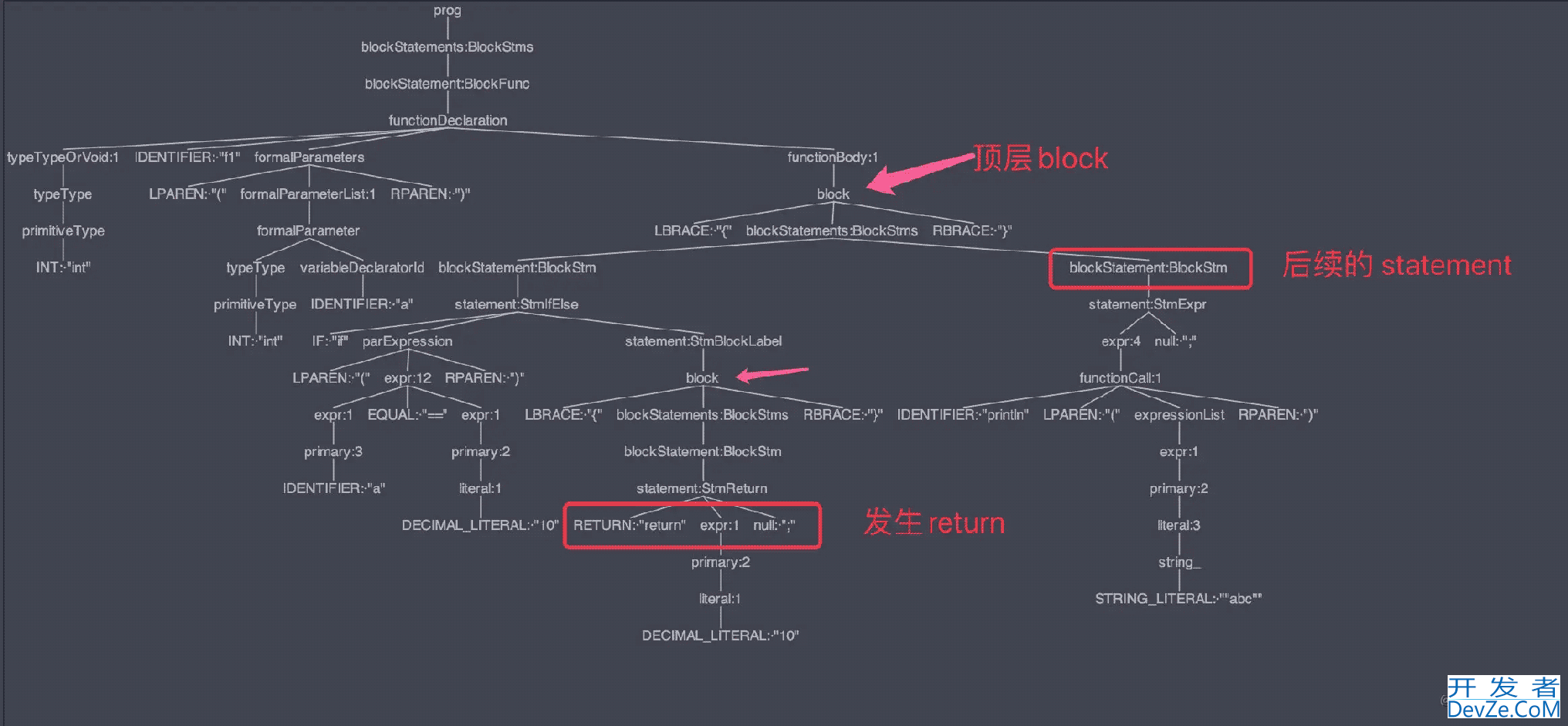
当碰到 return 语句的时,会递归向上遍历语法树,标记上所有 block 节点表明这个 block 后续的语句不再执行了,同时还得把返回值记录下来。
这样当执行到下一个 statement 时,也就是 println("abc"); 则会判断他所属的 block 是否有被标记,如果有则直接返回,这样便实现了 return 语句不执行后续代码。
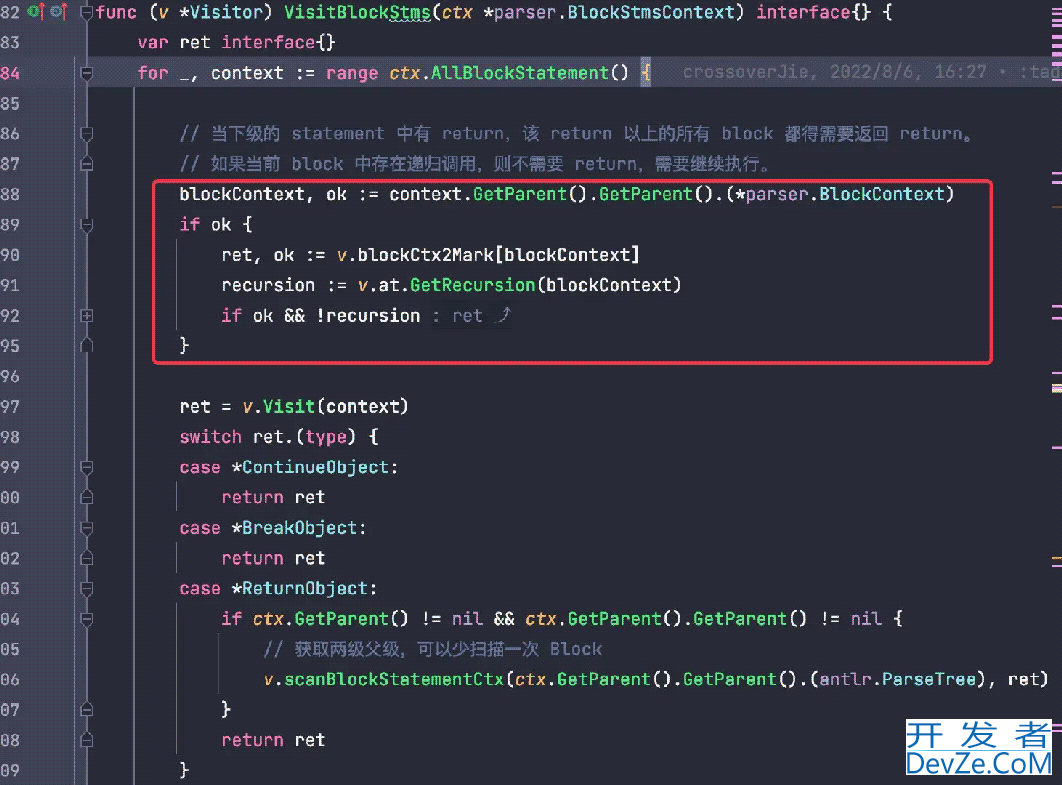
部分实现代码如下:
// 在 return 的时候递归向上扫描所有的 Block,并打上标记,用于后面执行 return 的时候直接返回。
func (v *Visitor) scanBlockStatementCtx(tree antlr.ParseTree, value interface{}) {
context, ok := tree.(*parser.BlockContext)
if ok {
if v.blockCtx2Mark == nil {
v.blockCtx2Mark = make(map[*parser.BlockContext]interface{})
}
v.blockCtx2Mark[context] = value
}
if tree.GetParent() != nil {
v.scanBlockStatementCtx(tree.GetParent().(antlr.ParseTree), value)
}
}
源码地址: github.com/crossoverJi…
递归的问题
但同时问题也来了,就是递归的时候也不会执行后续的递归代码了。
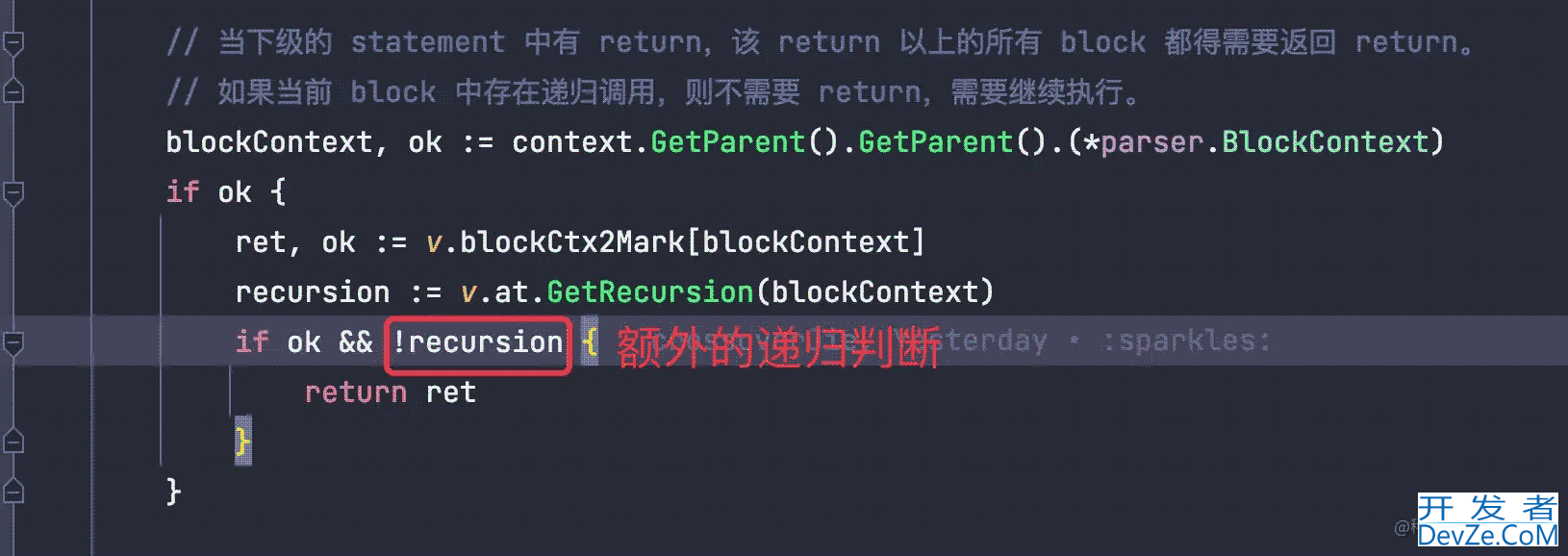
其实解决问题的方法也很简单,就是在判断是否需要直接返回那里新增一个条件,这个 block 中不存在递归调用。
所以我们就得先知道这个 block 中是否存在递归调用。
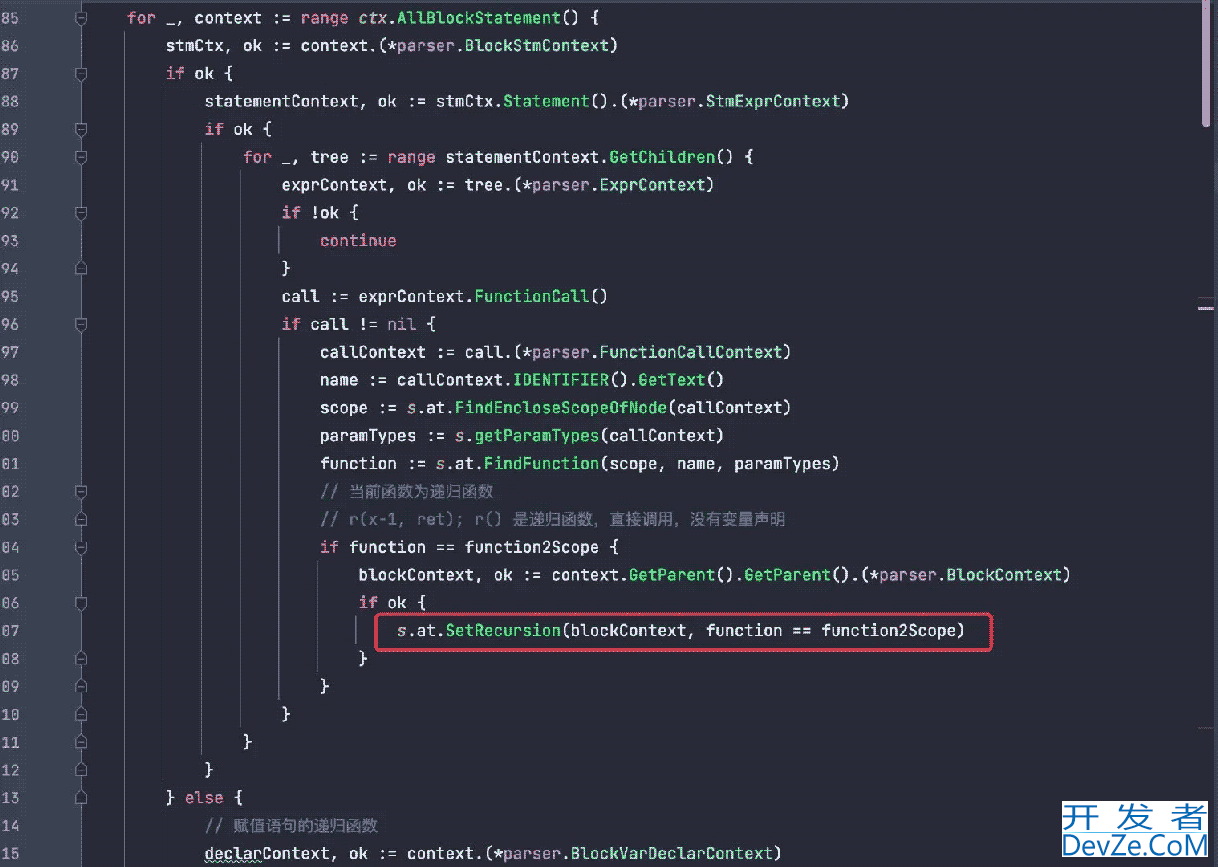
整个过程有以下几步:
- 编译期:在函数声明处记录下函数与当前
context的映射关系。 - 编译期:扫描
statement时,取出该statement的context所对应的函数。 - 编译期:扫描到的
statement如果是一个函数调用,则判断该函数是否为该block中的函数,也就是第二步取出的函数。 - 编译期:如果两个函数相等,则将当前
block标记为递归调用。 - 运行期:在刚才判断
return语句处,额外多出判断当前block是否为递归调用,如果是则不能返回。
部分代码如下:
github.com/crossoverJi…
总结
这里的递归调用其实卡了我挺长时间的,思路是有的,但是写出来的代码总是和预期不符,当天晚上坐在电脑面前到凌晨两三点,百思不得其解。
最后受不了上床休息的时候,突然一个灵光乍现让我想到了解决方案,于是第二天起了个早床赶忙实践,还真给解决了。
所以有些时候碰到棘手问题时给自己放松一下,往往会有出其不意的效果。
最后是目前的递归在某些情况下性能还有些问题,后续会尽量将这些标记过程都放在编译期,编译慢点没事,但运行时慢那就有问题了。
之后还会继续优化运行时的异常,目前是直接 panic,堆栈也没有,体感非常不好;欢迎感兴趣的朋友试用反馈bug。
源码地址:
github.com/crossoverJi…
以上就是go语言编程实现递归函数示例详解的详细内容,更多关于go 递归函数的资料请关注我们其它相关文章!





 加载中,请稍侯......
加载中,请稍侯......
精彩评论