基于Python实现拉格朗日插值法

目录

• 一、拉格朗日的基本思想
• 三、多个点
• 四、代码实现
• 五、完整代码
• 六、pop（）函数
• 七、结果展示

一、拉格朗日的基本思想

拉格朗日插值法是以法国十八世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。

许多实际问题中都用函数来表示某种内在联系或规律，而不少函数都只能通过实验和观测来了解。在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个简单函数,其恰好在各个现测的点取到观测到的值,这个函数可以是代数多项式,三角多项式等。

二、线性插值

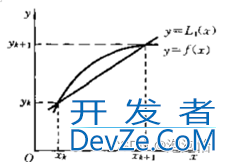
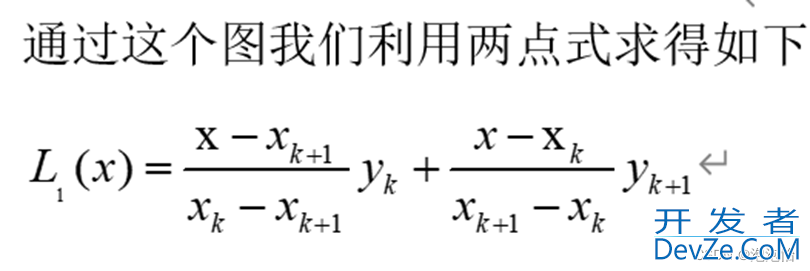
三、多个点

四、代码实现

def lagrange(xx,y):
    l=len(y)
    l_n = 0
    for k in range(l):
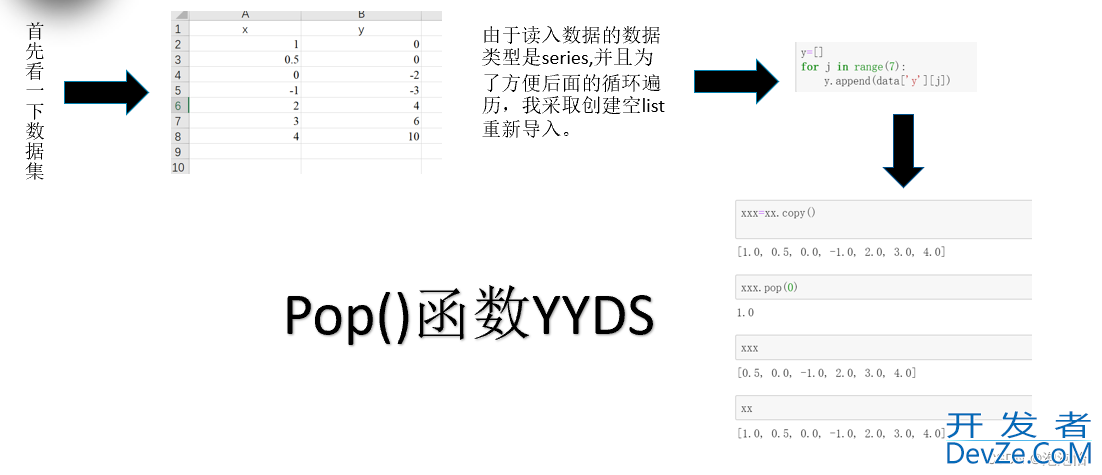
        xxx=xx.copy()
        x_k = xxx[k]
        xxx.pop(k)
        l_k = 1
        for i in range(len(xxx)):
            l_k *=android (x - xxx[i]) / (x_k -xxx[i])
        l_n += y[k] * l_k
    return expand(l_n) 

五、完整代码

import matplotlib.pyplot as plt
import numpy as np 
import pandas as pd
from sympy import expand
from sympy.abc import x
xx=[]
for i in range(7):
    xx.append(data['x'][i])
y=[]
for j in range(7):
    y.append(data['y'][j])
def lagrange(xx,y):
    l=len(y)
    l_n = 0
    for k in range(l):
        xxx=xx.copy()
        x_k = xxx[k]
        xxx.pop(k)
编程        l_k = 1
        for i in range(len(xxx)):
    javascript        l_k *= (x - xxx[i]) / (x_k -xxx[i])
        l_n += y[k] * l_k
    return expa开发者_JAVA学习nd(l_n)  
lagrange_interpolation_ppythonolynomial = lagrange(xx, y)
print("拉格朗日插值多项式为:",lagrange_interpolation_polynomial)
x2=np.编程客栈linspace(-1,4,100)
y1=[]
for i in range(len(x2)):
    y1.append(lagrange_interpolation_polynomial.subs(x,x2[i]))
print(y1)
#绘制散点图,逼近函数
plt.figure(figsize=(8,4))
plt.scatter(xx,y,c='red')
plt.plot(x2,y1,'-')
plt.show()

六、pop（）函数

七、结果展示

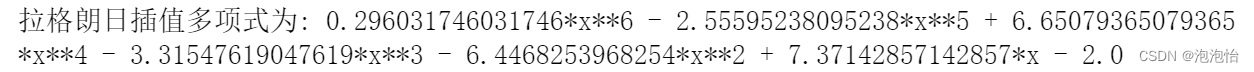
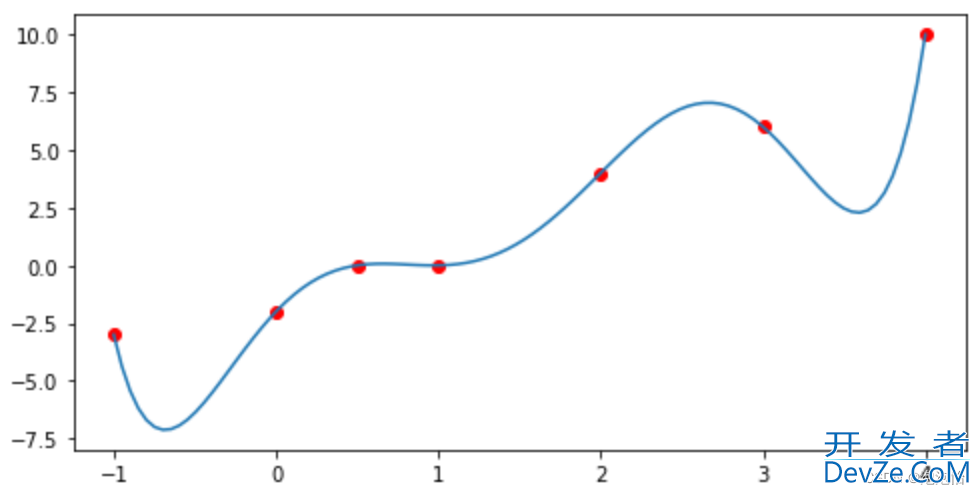
到此这篇关于基于python实现拉格朗日插值法的文章就介绍到这了,更多相关Python拉格朗日插值法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！