How to Prove one Random Number Generator is Better Than Another?

How do you prove that one RNG is better than another?

I don't mean in terms of runtime, but rather the amount of entropy "generated" - which also rolls in the notion of periodicity (low period = low entropy).

Can a RNG be provable optimal? Or is this an unobtainable goal? By optimal, I mean any sequence is equally likely and independent of past or future results.

I'm interested in algorithms, not cosmic background sampling devices or other sources of开发者_Go百科 physical "randomness" (is it random or just complex?)

---

See http://www.random.org/analysis/

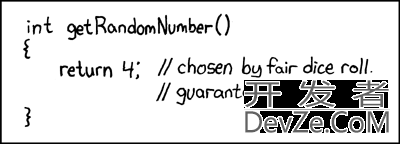
The one and only optimal RNG:

---

The National Institute of Standards and Technology has some good info on this:

http://csrc.nist.gov/groups/ST/toolkit/rng/index.html

Looks like there is a test suite and lots of good reference material

---

The old standard for testing used to be the "Diehard tests." http://en.wikipedia.org/wiki/Diehard_tests This has been superceded by the NIST tests that DKnight pointed out: http://csrc.nist.gov/groups/ST/toolkit/rng/index.html. The Diehard wiki article gives you a good overview of the kind of things that are looked at. The NIST bit will take a bit more digging.

As you state it, no pseudo RNG (algorithm) can be proven optimal. They all have a seed value and are dependent on the input to generate a value. If you know the seed and the state, you know the next value. As an example, check out http://en.wikipedia.org/wiki/Mersenne_twister. I like it mostly because of the awesome name, but the article does a good job explaining the tenets of a PRNG.

---

There is an objective definition from computational complexity theory: the asymptotic time complexity required to distinguish the output from random data.

A good PRNG should force a distinguisher to spend lots more time as the size of the seed increases or as the level of certainty required increases. (With fixed size seeds I suppose you'd look at the actual running time as well as the program complexity.)

• For comparing one PRNG against another, the one with a smaller/faster distinguisher is worse.
• One common assumption, even though it's not been proven, is that some PRNGs are indistinguishable from random in polynomial time. That's one possible meaning for 'optimal'.
• Statistical tests, like the diehard tests, are just simple distinguishers.

---

The basics are in Knuth, The Art of Computer Programming Vol 2, "Seminumerical algorithms". The idea is to devise tests of randomness where each test will try to find non-random aspects of a PRNG. Note that what might seem to be random to a human being is not. For instance, we tend to say that the sequence '1,4,4,1' for instance is non-random, whereas it may occur perfectly on a larger random sequence.

So the approach is roughly:

• Find different tests for randomness, this is essentially DieHard and NIST test groups.
• Execute said tests on the PRNG.
• If the PRNG fails one or more of the tests it can be perceived as a weaker PRNG than ones that survives.

A cool example of a test is phase-space analysis. Here is a link of it executed some years back on TCP randomness generators for different operating systems:

http://lcamtuf.coredump.cx/oldtcp/tcpseq.html

Other classical tests are chi-squares, Komolgorov-Smirnoff etc, all explained in Knuth. Good PRNGs survive any conceivable attack on them.

---

Generate sequences of numbers and then try to compress them. The more random ones will compress less. Pure randomness is incompressible. It would be interesting to see the results, and if there are going to be differences.