How to compute equations of this type (x^1+...x^n) in C#?

I have a math problem which is written like this:

x^1+x^2+x^3+...+x^n

Are there any constr开发者_如何学Cucts in C# that will help me solve these kinds of equations?

I know I could write a for loop or use recursion to accomplish this, but I remember reading about some construct in c# that will pre-compile such a statement for later execution.

Are there any interesting ways to solve these kinds of equations?

---

To calculate x^n use Math.Pow:

Math.Pow(x, n)

If you want to calculate the sum you could use a loop or LINQ. I don't think there's anything wrong with a simple loop here:

double total = 0;
for (int i = 1; i <= n; ++i)
{
    total += Math.Pow(x, i);
}
Console.WriteLine(total);

You can write this in LINQ but I don't see any particularly strong reason to do so. Perhaps you could expand on what features you are looking for? Are you looking for better performance?

Since your question is tagged 'mathematical-optimization' you might also want to optimize it by finding a shortcut. In this specific case it is a geometric series so you can use the formula:

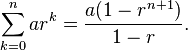
Or in C#:

static double geometricSeries(double a, double r, int n)
{
    return a * (1 - Math.Pow(r, n + 1)) / (1 - r);
}

In other more complex cases finding the formula might be more difficult.

---

I understand that your example is intentionally trivial. However, if what you're really trying to calculate is still a polynomial, then you should definitely use Horner scheme. Here's a C# implementation.

---

Well you might be talking about using a delegate for deferred execution. But in many cases it's the same as writing a method. For example, let's start with the "simple" way of doing it:

public static double SumExponents(double x, int n)
{
    double total = 0;
    for (int i = 1; i <= n; i++)
    {
         total += Math.Pow(x, i);
    }
    return total;
}

This can be written using LINQ as:

public static double SumExponents(double x, int n)
{
    return Enumerable.Range(1, n)
                     .Select(i => Math.Pow(x, i))
                     .Sum();
}

You could then write this as a single lambda expression:

Func<double, int, double> func = (x, n) => Enumerable.Range(1, n)
                                              .Select(i => Math.Pow(x, i))
                                              .Sum();

Is that the sort of thing you were thinking of? If not, please clarify your question. It's not really obvious what you're looking for.

---

There's nothing specific to C# about geometric progression. You can compute this sum in O(1) time. (Assuming power operation takes constant time.)

In your case, the formula would be

x*(x^n - 1)/(x - 1)

---

int total = 0;
for(int i = 1; i <= n; i++)
    total += Math.Pow(x, i);

---

As well as select\sum, you can also use Aggregate for folding sequences.

int n;
double x;
double result = Enumerable.Range(1, n)
    .Aggregate(0.0, (acc, i) => acc + Math.Pow(x, i));