Inverse of number in binary

Suppose we have some arbitrary positive number x.

I开发者_高级运维s there a method to represent its inverse in binary or x's inverse is 1/x - how does one express that in binary?

e.g. x=5 //101

x's inverse is 1/x, it's binary form is ...?

---

You'd find it the same way you would in decimal form: long division.

There is no shortcut just because you are in another base, although long division is significantly simpler.

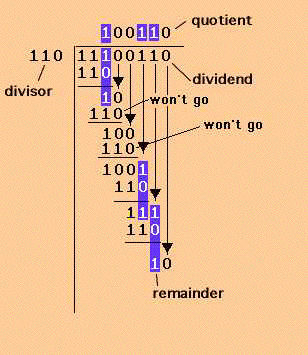
Here is a very nice explanation of long division applied to binary numbers.

Although, just to let you know, most floating-point systems on today's machines do very fast division for you.

---

In general, the only practical way to "express in binary" an arbitrary fraction is as a pair of integers, numerator and denominator -- "floating point", the most commonly used (and hardware supported) binary representation of non-integer numbers, can represent exactly on those fractions whose denominator (when the fraction is reduced to the minimum terms) is a power of two (and, of course, only when the fixed number of bits allotted to the representation is sufficient for the number we'd like to represent -- but, the latter limitation will also hold for any fixed-size binary representation, including the simplest ones such as integers).

---

0.125          = 0.001b
0.0625         = 0.0001b
0.0078125      = 0.0000001b
0.00390625     = 0.00000001b
0.00048828125  = 0.00000000001b
0.000244140625 = 0.000000000001b
----------------------------------
0.199951171875 = 0.001100110011b

Knock yourself out if you want higher accuracy/precision.

---

Another form of multiplicative inverse takes advantage of the modulo nature of integer arithmetic as implemented on most computers; in your case the 32 bit value 11001100110011001100110011001101 (-858993459 signed int32 or 3435973837 unsigned int32) when multiplied by 5 equals 1 (mod 4294967296). Only values which are coprime with the power of two the modulo operates on have such multiplicative inverses.

---

If you just need the first few bits of a binary fraction number, this trick will give you those bits: (2 << 31) / x. But don't use this trick on any real software project. (because it is rough, inaccurate and plainly wrong way to represent the value)