Mathematica: get number of arguments passed to a function?

How do I get the number of arguments passed to a function, such as Plus[2,3,4,5] has 4 arguments passed to it. I was thinking it may involve the use of the function Length and getting the arguments into a list. The intention is to iterate an operation based on the number of arguments for a function. There is probably a simple solution or function but I hav开发者_如何学Cen't come across it yet. Any other ways or suggestions are welcome as well?

---

Here's one way:

In[1]:= foo[args___] := Length[{args}]

In[2]:= foo[1,2,3,4]
Out[2]= 4

When you define a function like this, the pattern args___ (with 3 trailing underscores) will match a Sequence of 0 or more things. You can't use Length on a Sequence and have anything sensible happen, so you should wrap args in a List (the {}) first.

However, belisarius is correct. For a lot of iterative operations, it will be easier and more efficient to use built-in higher-order functions like Map and Fold.

EDIT to add: Due to way that Mathematica expressions are built on top of bounds-checked arrays, Length is O (1) in time. This might lead you to believe that foo also has O (1) complexity, but you would be wrong. Due to the way pattern-matching works, all of the elements matched by args will be copied into the new List that you then pass to Length, making the complexity O (N). This isn't necessarily a huge problem, because using really huge argument lists with a function almost invariably means using Apply, which does an O (N) copy anyway, but it's something you should know.

EDIT again to add: There's another way to do this using Length directly on the expression being evaluated (like most of Mathematica's list-oriented functions, Length can be used on expressions with any head, not just lists). Nothing is copied because no sequences are matched and given new heads, and the function which is having its arguments counted need not have any special attributes like HoldAll. Nonetheless, it is a sleazy hack that exploits a quirk in the pattern-matching machinery by introducing side-effects where side-effects really don't belong, so I would use it with extreme caution, if at all:

Module[{n},
 expr : foo[___] /; (n = Length[Unevaluated[expr]]; True) :=
  n]

The variable n could be global, but Module will create (or at least do a good job faking) lexical closures, so you can at least keep your variables local.

---

I think that you are going to have to start intefering with Mathematica's evaluation sequence or, possibly simpler, interfering with the properties of its intrinsic functions. One of the problems you have is that Mathematica evaluates very greedily, so by the time you have pressed return after entering Plus[2,3,4,5] it has done its stuff and returned 14.

You could possibly fiddle with $Pre to achieve what you want. But you might have to Unprotect[Plus] and force it to Hold its arguments until you've had a chance to count how many there are.

Of course, if you were just using Plus as an example and really want to define a function of your own then your task is probably a lot easier. Here is a function I wrote which simply returns the number of arguments it gets:

fun[y___]:=Length[{y}]

I've tested this on some simple cases. It will be instructive for you to try things like:

fun[1,{2,3}]

I tend to agree with the comment already made, that what you propose to do is not very Mathematica-al

---

Per my comments in another answer, the idiomatic way to do this is typically:

Length[Unevaluated[expr]]

E.g.:

In[1]:= Length[Unevaluated[Plus[1, 2, 3, 4]]]

Out[1]= 4

The use of Unevaluated prevents the argument from evaluating, avoiding the situation where the argument to Length (which does not have any Hold* attributes) would evaluate to an atomic value (like a number) which doesn't have a length, and Length returns 0 in such cases:

In[2]:= Length[Plus[1, 2, 3, 4]]

Out[2]= 0

---

You can always use lists:

f[list_]:= (len = Length[list];
            While [....
                   do whatever
                 ];
            Return [ ..];
           );

 myOut= f[{a,b,c}];

This way is appropriate to use with Mathematica because list management is very powerful.

If you use f[a,b,c], the number of arguments is hard-coded

But again ... try the functional way.

---

Not sure what kind of recursion you need, but in my experience a (Haskel inspired?) first,rest pattern in your function definition can be quite powerful:

f[onearg_]:=onearg
f[first_,rest__]:=first+2 f[rest]

In[148]= Trace@f[2,3,4]
Out[148]= {f[2,3,4],2+2 f[3,4],{{f[3,4],3+2 f[4],{{f[4],4},2 4,8},3+8,11},2 11,22},2+22,24}

And of course, you have access to Length[{rest}] if you need it.

EDIT 2: (Old plot was incorrect as pointed out by Pilsy) Mathematica actually copies the 'rest' part, so that the scaling turns quadratic if the cost of the actual function is negligible.

f[] := 0;
f[onearg_] := onearg[[1, 1]];
f[first_, rest__] := f[first] + f[rest];
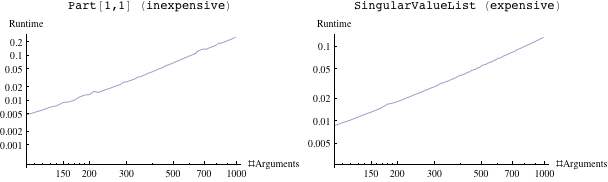
ListLogLogPlot[Part[#, -1, 1],
   Joined -> True, PlotRange -> {{100, All}, Automatic}, 
   AxesLabel -> {"#Arguments", "Runtime"}] &@
 Reap@Nest[
   Function[all, 
    Sow[{Length[all], First@Timing[Table[f @@ all, {10}]]}];
    Join[all, RandomReal[{-1, 1}, {10, 10, 10}]]], {}, 100]

The figure below shows the output for an inexpensive inner function f[onearg_]:=onearg[[1,1]] as above where the scaling is indeed quadratic in number of arguments, and for an expensive inner function f[onearg_]:=SingularValueList[onearg,1], where the scaling is closer to linear.

---

Some of the solutions above require that you input the arguments explicitly into a function which puts it in a list. With my own study I have found there is way to calculate the answer. Given the expression 3 + 2*2*2*4 + 5, find how many arguments are passed to the Times function. With a bit of help visualising it with the TreeForm function, I put together some of mathematica's built in functions to evaluate an answer.

Steps:
1/ Get position of the function.
2/ It returns a nested list.
3/ Flatten list.
4/ Get list's length which will be the level that the arguments of the function are at.
5/ Level returns a list of the arguments which you can then get the length of.

Example:

In[89]:= Position[Hold[3 + 2*2*2*4 + 5], Times]

Out[89]= (1    2    0)

In[90]:= FullForm[%]

Out[90]= List[List[1,2,0]]

In[91]:= Flatten[%]

Out[91]= {1,2,0}

In[92]:= FullForm[%]

Out[92]= List[1,2,0]

In[93]:= Length[%]

Out[93]= 3

In[94]:= Level[Hold[3 + 2*2*2*4 + 5], {%}]

Out[94]= {2,2,2,4}

In[95]:= Length[%]

Out[95]= 4

This could all be put in a function. Though it may not handle the case when there are two instances of the same function within an expression in an automated way. This may require some condition set or input by the user.