Sample uniformly at random from an n-dimensional unit simplex_问答_开发者

Sampling uniformly at random from an n-dimensional unit simplex is the fancy way to say that you want n random numbers such that

they are all non-negative,
they sum to one, and
every possible vector of n non-negative numbers that sum to one are equally likely.

In the n=2 case you want to sample uniformly from the segment of the line x+y=1 (ie, y=1-x) that is in the positive quadrant. In the n=3 case you're sampling from the triangle-shaped part of the plane x+y+z=1 that is in the positive octant of R3:

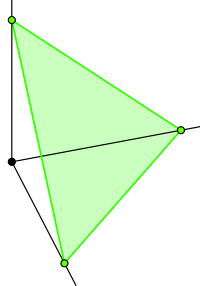
(Image from http://en.wikipedia.org/wiki/Simplex.)

Note that picking n uniform random numbers and then normalizing the开发者_运维知识库m so they sum to one does not work. You end up with a bias towards less extreme numbers.

Similarly, picking n-1 uniform random numbers and then taking the nth to be one minus the sum of them also introduces bias.

Wikipedia gives two algorithms to do this correctly: http://en.wikipedia.org/wiki/Simplex#Random_sampling (Though the second one currently claims to only be correct in practice, not in theory. I'm hoping to clean that up or clarify it when I understand this better. I initially stuck in a "WARNING: such-and-such paper claims the following is wrong" on that Wikipedia page and someone else turned it into the "works only in practice" caveat.)

Finally, the question: What do you consider the best implementation of simplex sampling in Mathematica (preferably with empirical confirmation that it's correct)?

Related questions

Generating a probability distribution
java random percentages

This code can work:

samples[n_] := Differences[Join[{0}, Sort[RandomReal[Range[0, 1], n - 1]], {1}]]

Basically you just choose n - 1 places on the interval [0,1] to split it up then take the size of each of the pieces using Differences.

A quick run of Timing on this shows that it's a little faster than Janus's first answer.

After a little digging around, I found this page which gives a nice implementation of the Dirichlet Distribution. From there it seems like it would be pretty simple to follow Wikipedia's method 1. This seems like the best way to do it.

As a test:

In[14]:= RandomReal[DirichletDistribution[{1,1}],WorkingPrecision->25]
Out[14]= {0.8428995243540368880268079,0.1571004756459631119731921}
In[15]:= Total[%]
Out[15]= 1.000000000000000000000000

A plot of 100 samples:

alt text http://www.public.iastate.edu/~zdavkeos/simplex-sample.png

I'm with zdav: the Dirichlet distribution seems to be the easiest way ahead, and the algorithm for sampling the Dirichlet distribution which zdav refers to is also presented on the Wikipedia page on the Dirichlet distribution.

Implementationwise, it is a bit of an overhead to do the full Dirichlet distribution first, as all you really need is n random Gamma[1,1] samples. Compare below
Simple implementation

SimplexSample[n_, opts:OptionsPattern[RandomReal]] :=
  (#/Total[#])& @ RandomReal[GammaDistribution[1,1],n,opts]

Full Dirichlet implementation

DirichletDistribution/:Random`DistributionVector[
 DirichletDistribution[alpha_?(VectorQ[#,Positive]&)],n_Integer,prec_?Positive]:=
    Block[{gammas}, gammas = 
        Map[RandomReal[GammaDistribution[#,1],n,WorkingPrecision->prec]&,alpha];
      Transpose[gammas]/Total[gammas]]

SimplexSample2[n_, opts:OptionsPattern[RandomReal]] := 
  (#/Total[#])& @ RandomReal[DirichletDistribution[ConstantArray[1,{n}]],opts]

Timing

Timing[Table[SimplexSample[10,WorkingPrecision-> 20],{10000}];]
Timing[Table[SimplexSample2[10,WorkingPrecision-> 20],{10000}];]
Out[159]= {1.30249,Null}
Out[160]= {3.52216,Null}

So the full Dirichlet is a factor of 3 slower. If you need m>1 samplepoints at a time, you could probably win further by doing (#/Total[#]&)/@RandomReal[GammaDistribution[1,1],{m,n}].

Here's a nice concise implementation of the second algorithm from Wikipedia:

SimplexSample[n_] := Rest@# - Most@# &[Sort@Join[{0,1}, RandomReal[{0,1}, n-1]]]

That's adapted from here: http://www.mofeel.net/1164-comp-soft-sys-math-mathematica/14968.aspx (Originally it had Union instead of Sort@Join -- the latter is slightly faster.)

(See comments for some evidence that this is correct!)

I have created an algorithm for uniform random generation over a simplex. You can find the details in the paper in the following link: http://www.tandfonline.com/doi/abs/10.1080/03610918.2010.551012#.U5q7inJdVNY

Briefly speaking, you can use following recursion formulas to find the random points over the n-dimensional simplex:

x₁=1-R₁^1/n-1

x_k=(1-Σ_i=1^kx_i)(1-R_k^1/n-k), k=2, ..., n-1

x_n=1-Σ_i=1^n-1x_i

Where R_i's are random number between 0 and 1.

Now I am trying to make an algorithm to generate random uniform samples from constrained simplex.that is intersection between a simplex and a convex body.

Old question, and I'm late to the party, but this method is much faster than the accepted answer if implemented efficiently.

In Mathematica code: #/Total[#,{2}]&@Log@RandomReal[{0,1},{n,d}]

In plain English, you generate n rows * d columns of randoms uniformly distributed between 0 and 1. Then take the Log of everything. Then normalize each row, dividing each element in the row by the row total. Now you have n samples uniformly distributed over the (d-1) dimensional simplex.

If found this method here: https://mathematica.stackexchange.com/questions/33652/uniformly-distributed-n-dimensional-probability-vectors-over-a-simplex

I'll admit, I'm not sure why it works, but it passes every statistical test I can think of. If anyone has a proof of why this method works, I'd love to see it!