What is a parity check matrix? (Information theory)

I'm studying information theory but one thing I can't seem to work out.

I know that given a linear code C and a generator开发者_StackOverflow社区 matrix M I can work out all the possible codewords of C.

However I do not understand:

• What a parity check matrix is http://en.wikipedia.org/wiki/Parity-check_matrix
• How to make a parity check matrix from a generator matrix

I'd really appreciate any pointers!

Thanks!

---

I think your link explains it fairly well, but I'll try to simplify further.

Let x be your message, a k-element row vector. Let G be your generator matrix, an k-by-n binary matrix where n > k. Let y be your n-element transmitted codeword where y = xG. Let z be your n-element received codeword.

Hopefully, z = y. But when transmitting y across a noisy channel, it is possible for y to become corrupted, e.g., z != y.

An (n-k)-by-n parity matrix H is applied to the received codeword z to check if z is valid. The vector w = zH' can detect up to a certain number of bit errors in z.

---

In coding theory, a parity-check matrix of a linear block code C is a generator matrix of the dual code. As such, a codeword c is in C if and only if the matrix-vector product Hc=0.

The rows of a parity check matrix are parity checks on the codewords of a code. That is, they show how linear combinations of certain digits of each codeword equal zero. For example, the parity check matrix

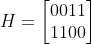
specifies that for each codeword, digits 1 and 2 should sum to zero (according to the second row) and digits 3 and 4 should sum to zero.

---

LDPC i believe uses parity check matrix. more generally error control/correction algorithms