What would be the time complexity of counting the number of all structurally different binary trees?

Using the method presented here: http://cslibrary.stanford.edu/110/BinaryTrees.html#java

12. countTrees() Solution (Java)
/**
 For the key values 1...numKeys, how many structurally unique
 binary search trees are possible that store those keys?

 Strategy: consider that each value could be the root.
 Recursively find the size of the left and right subtrees.
*/
public static int countTrees(int numKeys) {
  if (numKeys <=1) {
    return(1);
  }
  else {
    // there will be one value at the root, with whatever remains
    // on the left and right each forming their own subtrees.
    // Iterate through all the values that c开发者_开发百科ould be the root...
    int sum = 0;
    int left, right, root;

    for (root=1; root<=numKeys; root++) {
      left = countTrees(root-1);
      right = countTrees(numKeys - root);

      // number of possible trees with this root == left*right
      sum += left*right;
    }

    return(sum);
  }
} 

I have a sense that it might be n(n-1)(n-2)...1, i.e. n!

If using a memoizer, is the complexity O(n)?

---

The number of full binary trees with number of nodes n is the nth Catalan number. Catalan Numbers are calculated as

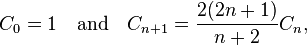
which is complexity O(n).

http://mathworld.wolfram.com/BinaryTree.html

http://en.wikipedia.org/wiki/Catalan_number#Applications_in_combinatorics

---

It's easy enough to count the number of calls to countTrees this algorithm uses for a given node count. After a few trial runs, it looks to me like it requires 5*3^(n-2) calls for n >= 2, which grows much more slowly than n!. The proof of this assertion is left as an exercise for the reader. :-)

A memoized version required O(n) calls, as you suggested.

Incidentally, the number of binary trees with n nodes equals the n-th Catalan number. The obvious approaches to calculating C_n all seem to be linear in n, so a memoized implementation of countTrees is probably the best one can do.

---

Not sure of how many hits to the look-up table is the memoized version going to make (which is definitely super-linear and will have the overheads of function calling) but with the mathematical proof yielding the result to be the same as nth Catalan number, one can quickly cook up a linear-time tabular method:

    int C=1;
    for (int i=1; i<=n; i++)
    {
        C = (2*(2*(i-1)+1)*C/((i-1)+2));
    }
    return C;

Note the difference between Memoization and Tabulation here