"(1:k) Tree-Matching" - Solvable in polynomial time?

Some months ago there was a nice question regarding a "1:n matching problem" and there see开发者_如何学Cms to be no poly-time algorithm.

I would like to add constraints to find a maximum matching for the 1:n matching problem with a polynomial algorithm. I would like to say: "For vertex A1 choose either {B1,B2,B5} or {B2,B3} if the vertices are not already taken from another A-vertex" i.e. I would not allow all possible combinations.

This could be expressed if we introduce helper vertices H for each choice and substitute edges with trees => we get a problem similar to the ordinary bipartite matching. Every vertex of A or B can have only one edge in the matching. The edges to or from vertices in H are either all in the matching or none of them is present in the matching. Imagine the following tri-partite graph:

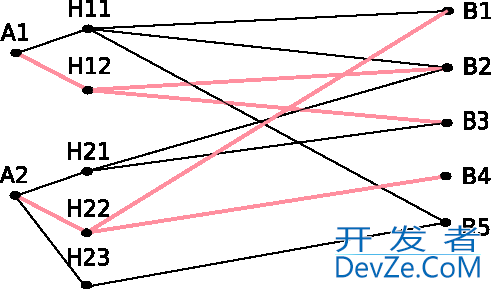
Now define h_ij="tree rooted that contains H_ij" to express the matching easily:

• Then in the example M={h12,h22} would be one 'maximum' matching, although not all vertices from B are involved
• The set {h12,h23} is not a matching because then B3 would have be choosen twice.

Would this problem then be solvable in polynomial time? If yes, is there a polytime solution for the weighted (w(h_ij)) variant? If no, could you argue or even proof it for a "simple-man" like me or suggest other constraints to solve the 1:n matching problem?

E.g. could the graph transformed to a general graph which then could be solved with the weighted matching for general graphs? Or could branchings or even matching forests help here?

PS: not a homework ;-)

---

There is a difference between maximal and maximum. I have assumed you meant maximum for the below writeup.

You don't seem to have defined your problem very clearly, but if I have understood your intent correctly, It seems like your problem is NP complete (and 'equivalent' to Set Packing).

We can assume that the allowed sets sizes is the same (k) for all A_i to find a [1:k] matching, as any other set size can be ignored. To find max k, we just run the algorithm for [1:k] for k = 1,2,3.. etc.

So your problem is (I think...):

Given m set families F_i = {S_1i, .., S_n(i)i} (|F_i| = size of F_i = n(i), need not be same as |F_j|), each set of size k, you have to find one set from each family (say S_i) such that

• S_i and S_j are disjoint for any i neq j.
• number of S_i's is maximum.

We can show that it is NP-Complete for k=3 in two steps:

1. The NP-Complete problem Set Packing can be reduced it. This shows that it is NP-Hard.
2. Your problem is in NP and can be reduced to Set Packing. This and 1) implies your problem is NP-Complete. It also helps you leverage any approximation/randomized algorithms already existing for Set-Packing.

Set Packing is the problem:

Given n sets S_1, S_2, ..., S_n, find the maximum number of pairwise disjoint sets among these.

This problem remains NP-Complete even if |S_1| = |S_2| = ... = |S_n| = 3 and is called the 3-Set packing problem.

We will use this to show that your problem is NP-Hard, by providing an easy reduction from 3-Set packing to your problem.

Given S_1, S_2, .., S_n just form the families

F_i = {S_i}.

Now if your problem had a polynomial time solution, then we get a set of Sets {S_1, S_2, ..., S_r} such that

• S_i and S_j are disjoint
• Number of S_i is maximum.

This easy reduction gives us a solution to the 3-set Packing problem and thus your problem is NP-Hard.

To see that this problem is in NP, we reduce it to Set-Packing as follows:

Given F_i = {S_1i, S_2i, ..., S_ni}

we consider the sets T_ji = S_ji U {i} (i.e. we add an id of the family into the set itself) and run them through the Set-Packing algorithm. I will leave it to you to see why a solution to Set-Packing gives a solution to your problem.

---

For a maximal solution, all you need is a greedy algorithm. Just keep picking up sets till you can pick no more. This would be polynomial time.