How to find the center of gravity or center of mass of an irregular body with uniform mass distribution?

Recently I was trying to solve a small AI problem but got stuck in between as I could not find the center of mass of the various bodies. I was wondering if any one of you could help me out with this one.

Problem explanation: Assume that i have a 2D body which is very irr开发者_如何学编程egular in shape and has a uniform mass distribution throughout. It's like the body is made up of 'n' tiny particles each of unit mass and hence though the body is very irregular in shape but the mass distribution is uniform. How can I locate the center of mass or center of gravity of this body?

Avanish!!

---

Calculating a polygon's center of mass:

Simplify your body into a polygon, and find its centroid, because (quoting wikipedia):

If an object has uniform density then its center of mass is the same as the centroid of its shape.

This approach is faster if there are lots of particles, uniformly distributed within the polygon.

Calculating the mean location of all particles:

If you're having n particles, calculate the mean of their X and Y coordinates; That's the center of mass.

Quoting wikipedia again:

The center of mass of a system of particles is defined as the average of their positions, weighted by their masses:

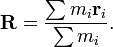
Your particles have the same mass, so your denominator equals n. The code in @tkerwin's answer calculates that fraction.

This approach works well if you don't have too many particles.

Edit:

Probabilistic calculation:

If you have too many points to efficiently calculate their mean location, try picking up some random points. Calculating their mean location would give you an excellent approximation of the entire mean. The more points you pick, the better is your approximation - according to the Law Of Large Numbers.

---

The center of mass is the average position of each particle weighted by the mass of that particle. Since your particles are of the same mass, you only need to take the average position.

That is:

center_x = 0
center_y = 0
for p in particles:
    center_x += p.x
    center_y += p.y
center_x /= len(particles)
center_y /= len(particles)

---

OK. I get it now. You have a vast number of discrete particles to work with. With emphasis on the big number.

Well, why didn't you say?

You can't do it exactly (i.e. without approximation) any faster than iterating though all the points. At least not without providing more relevant information.

Adam's sampling suggestion is a good way to obtain an approximation if you have random access to the data.

An alternative that won't be faster for a single operation, but might be useful if you are going to have to recalculate often is to reduce the working set to a smaller group of heavier points. Something like this:

1. Divide space into a grid of N_x * N_y * N_z cells of sizes (l_x,l_y,L_z).
2. Compute the total mass and location of the center of mass for all the points in each cell.
3. Discard any cells with no points contained, and use the results as the new working set.

For this to represent an improvement, you'll want to have an average of 10 or more original points per cell, but not so many that the introduced grandularity washes out the signal you are looking for.

How best to do step 2 depends on how the original data is organized and on how much room you have in memory to store intermediate results. With lots of memory available:

• Prepare and initialize to zero four (N_x,N_y,N_z) arrays called M, Rx, Ry, and Rz (or one scalar array M and one vector array R, that depends on your implementation language)
• Walk the main list on time, incrementing the values in the appropriate cell for each mass
• Walk the intermediate arrays to figure the collected masses and locations.

With relatively little memory but lots of time available for pre-calculation you would walk the main list once for every cell (but if you have that kind of time you probable can just do this straight).