Efficient implementation of mutual information in Java_问答_开发者

I'm looking to calculate mutual information between two features, using Java.

I've read Calculating Mutual Information For Selecting a Training Set in Java already, but that was a discussion of if mutual information was appropriate for the poster, with only some light pseudo-code as to the implementation.

My current code is below, but I'm hoping there is a way to optimise it, as I have large quantities of information to process. I'm aware that calling out to another language/framework may improve speed, but would like to focus on solving this in Java for now.

Any help much appreciated.

public static double calculateNewMutualInformation(double frequencyOfBoth, dou开发者_运维知识库ble frequencyOfLeft,
                                                   double frequencyOfRight, int noOfTransactions) {
    if (frequencyOfBoth == 0 || frequencyOfLeft == 0 || frequencyOfRight == 0)
        return 0;
    // supp = f11
    double supp = frequencyOfBoth / noOfTransactions; // P(x,y)
    double suppLeft = frequencyOfLeft / noOfTransactions; // P(x)
    double suppRight = frequencyOfRight / noOfTransactions; // P(y)
    double f10 = (suppLeft - supp); // P(x) - P(x,y)
    double f00 = (1 - suppRight) - f10; // (1-P(y)) - P(x,y)
    double f01 = (suppRight - supp); // P(y) - P(x,y)

    // -1 * ((P(x) * log(Px)) + ((1 - P(x)) * log(1-p(x)))
    double HX = -1 * ((suppLeft * MathUtils.logWithoutNaN(suppLeft)) + ((1 - suppLeft) * MathUtils.logWithoutNaN(1 - suppLeft)));
    // -1 * ((P(y) * log(Py)) + ((1 - P(y)) * log(1-p(y)))
    double HY = -1 * ((suppRight * MathUtils.logWithoutNaN(suppRight)) + ((1 - suppRight) * MathUtils.logWithoutNaN(1 - suppRight)));

    double one = (supp * MathUtils.logWithoutNaN(supp)); // P(x,y) * log(P(x,y))
    double two = (f10 * MathUtils.logWithoutNaN(f10)); 
    double three = (f01 * MathUtils.logWithoutNaN(f01));
    double four = (f00 * MathUtils.logWithoutNaN(f00));
    double HXY = -1 * (one + two + three + four);
    return (HX + HY - HXY) / (HX == 0 ? MathUtils.EPSILON : HX);
}        

public class MathUtils {
public static final double EPSILON = 0.000001;

public static double logWithoutNaN(double value) {
    if (value == 0) {
        return Math.log(EPSILON);
    } else if (value < 0) {
        return 0;
    }
    return Math.log(value);
}

I have found the following to be fast, but I have not compared it against your method - only that provided in weka.

It works on the premise of re-arranging the MI equation so that it is possible to minimise the number of floating point operations:

$Efficient implementation of mutual information in Java$

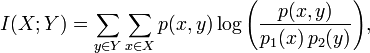
We start by defining $p(\cdot)$ as count/frequency over number of samples/transactions. So, we define the number of items as n, the number of times x occurs as |x|, the number of times y occurs as |y| and the number of times they co-occur as |x,y|. We then get,

$MI(X;Y) = \sum \limits_{y \in Y} \sum \limits_{x \in X} \frac{|x,y|}{n} \log \frac{\frac{|x,y|}{n}}{\frac{|x|}{n}\frac{|y|}{n}}$ .

Now, we can re-arrange that by flipping the bottom of the inner divide, this gives us (n|x,y|)/(|x||y|). Also, compute use N = 1/n so we have one less divide operation. This gives us:

$MI(X;Y) = \sum \limits_{y \in Y} \sum \limits_{x \in X} N|x,y| log \bigg(\frac{n|x,y|}{|x||y|} \bigg)$

This gives us the following code:

/***
 * Computes MI between variables t and a. Assumes that a.length == t.length.
 * @param a candidate variable a
 * @param avals number of values a can take (max(a) == avals)
 * @param t target variable
 * @param tvals number of values a can take (max(t) == tvals)
 * @return 
 */
static double computeMI(int[] a, int avals, int[] t, int tvals) {
    double numinst = a.length;
    double oneovernuminst = 1/numinst;
    double sum = 0;

    // longs are required here because of big multiples in calculation
    long[][] crosscounts = new long[avals][tvals];
    long[] tcounts = new long[tvals];
    long[] acounts = new long[avals];
    // Compute counts for the two variables
    for (int i=0;i<a.length;i++) {
        int av = a[i];
        int tv = t[i];
        acounts[av]++;
        tcounts[tv]++;
        crosscounts[av][tv]++;
    }

    for (int tv=0;tv<tvals;tv++) {
        for (int av=0;av<avals;av++) {
            if (crosscounts[av][tv] != 0) {
                // Main fraction: (n|x,y|)/(|x||y|)
                double sumtmp = (numinst*crosscounts[av][tv])/(acounts[av]*tcounts[tv]);
                // Log bit (|x,y|/n) and update product
                sum += oneovernuminst*crosscounts[av][tv]*Math.log(sumtmp)*log2;
            }
        }

    }

    return sum;
}

This code assumes that the values of a and t are not sparse (i.e. min(t)=0 and tvals=max(t)) for it to be efficient. Otherwise (as commented) large and unnecessary arrays are created.

I believe this approach improves further when computing MI between several variables at once (the count operations can be condensed - especially that of the target). The implementation I use is one that interfaces with WEKA.

Finally, it might be more efficient even to take the log out of the summations. But I am unsure whether log or power will take more computation within the loop. This is done by:

Apply a*log(b) = log(a^b)
Move the log to outside the summations, using log(a)+log(b) = log(ab)

and gives:

$MI(X;Y) = \log \bigg[ \prod \limits_{y \in Y} \prod \limits_{x \in X} \bigg(\frac{n|x,y|}{|x||y|}\bigg)^{\frac{|x,y|}{n}} \bigg]$

I am not mathematician but..

There are just a bunch of floating point calculations here. Some mathemagician might be able to reduce this to fewer calculation, try the Math SE.

Meanwhile, you should be able to use a static final double for Math.log(EPSILON)

Your problem might not be a single call but the volume of data for which this calculation has to be done. That problem is better solved by throwing more hardware at it.